题目内容
12.如图是某平面图形的直观图,则原平面图形的面积是( )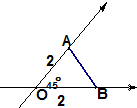
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 8 |
分析 利用三角形面积公式求出直观图的面积,进而根据$\frac{{S}_{原图}}{{S}_{直观图}}$=2$\sqrt{2}$,得到答案.
解答 解:由已知中的图象可得:直观图的面积为:$\frac{1}{2}$×2×2×sin45°=$\sqrt{2}$,
由$\frac{{S}_{原图}}{{S}_{直观图}}$=2$\sqrt{2}$,
可得原图面积为:4,
故选:A
点评 本题考查了水平放置的平面图形的直观图的画法,考查了原图形和直观图面积之间的关系,最好记住结论:$\frac{{S}_{原图}}{{S}_{直观图}}$=2$\sqrt{2}$,该题是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知点M(4,5)是⊙O:x2+y2-6x-8y=0内一点,则以点M为中点的圆O的弦长为( )
| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{17}$ | C. | 2$\sqrt{23}$ | D. | 6 |
3.已知x>0,函数y=$\frac{4}{x}$+x的最小值是( )
| A. | $2\sqrt{2}$ | B. | 4 | C. | -4 | D. | -$2\sqrt{2}$ |
7.函数f(x)=ax3-x在R上为减函数,则( )
| A. | a≤0 | B. | a<1 | C. | a<0 | D. | a≤1 |
1.400°角终边所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |