题目内容

3．已知x＞0，函数y=$\frac{4}{x}$+x的最小值是（　　）
A．$2\sqrt{2}$B．4C．-4D．-$2\sqrt{2}$

分析 由题意和基本不等式可得y=$\frac{4}{x}$+x≥2$\sqrt{x•\frac{4}{x}}$=4，验证等号成立即可．

解答 解：∵x＞0，∴y=$\frac{4}{x}$+x≥2$\sqrt{x•\frac{4}{x}}$=4，
当且仅当$\frac{4}{x}$=x即x=2时，y最最小值4
故选：B．

点评 本题考查基本不等式求最值，属基础题．

练习册系列答案
相关题目
13．设α，β是关于x的方程x2+2x+m=0（m∈R）的两个根，则|α|+|β|的值为$\left\{\begin{array}{l}{2，（0≤m≤1）}\\{2\sqrt{1-m}，（m＜0）}\end{array}\right.$．．
14．已知a，b，c分别是△ABC的三个内角A，B，C所对的边，若a=1，b=$\sqrt{3}$，A+C=2B，则sinC=（　　）
A．1B．$\frac{1}{2}$C．$\frac{{\sqrt{2}}}{2}$D．$\frac{{\sqrt{3}}}{2}$
11．在△ABC中，角A、B、C的对边依次为a，b，c且cos2A+3cosA-1=0．
（Ⅰ）求A；
（Ⅱ）若a=$\sqrt{13}$，△ABC的面积是3$\sqrt{3}$，求b+c的值．
18．已知函数f（x）=$\frac{1}{2}a{x^2}$+2x，g（x）=lnx．
（1）设函数F（x）=f（x）-g（x），若F（x）在$[\frac{1}{2}，+∞）$上单调递增，求a的取值范围；
（2）是否存在实数a＞0，使得方程$\frac{g（x）}{x}$=f′（x）-（2a+1）在区间$（\frac{1}{e}，e）$内有且只有两个不相等的实数根？若存在，请求出a的取值范围；若不存在，请说明理由．
8．现有l位教师，2位男同学，3位女同学共6人站成一排，则2位男同学站首尾两端，且3位女同学中有且仅有两位相邻的概率为（　　）
A．$\frac{1}{10}$B．$\frac{1}{20}$C．$\frac{1}{30}$D．$\frac{1}{60}$
15．平面内给定三个向量：$\overrightarrow{a}$=（3，2），$\overrightarrow{\;}$b=（-1，2），$\overrightarrow{c}$=（4，1）．
（1）求3$\overrightarrow{a}$+$\overrightarrow{b}$-2$\overrightarrow{c}$；
（2）若（$\overrightarrow{a}$+k$\overrightarrow{c}$）∥（2$\overrightarrow{b}$-$\overrightarrow{a}$），求实数k．
12．如图是某平面图形的直观图，则原平面图形的面积是（　　）
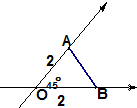
A．4B．2$\sqrt{2}$C．4$\sqrt{2}$D．8
13．若△ABC的内角A，B满足$\frac{sinB}{sinA}$=2cos（A+B），则当B取最大值时，角C大小为$\frac{2π}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网