题目内容
2.(x+2y)7的展开式中系数最大的项等于672x2y5.分析 设r+1项系数最大,则有$\left\{\begin{array}{l}{{C}_{7}^{r}•{2}^{r}≥{C}_{7}^{r-1}•{2}^{r-1}}\\{{C}_{7}^{r}•{2}^{r}≥{C}_{7}^{r+1}•{2}^{r+1}}\end{array}\right.$,求出r,即可求出系数最大项.
解答 解:设r+1项系数最大,则有$\left\{\begin{array}{l}{{C}_{7}^{r}•{2}^{r}≥{C}_{7}^{r-1}•{2}^{r-1}}\\{{C}_{7}^{r}•{2}^{r}≥{C}_{7}^{r+1}•{2}^{r+1}}\end{array}\right.$,
解得$\frac{13}{3}≤r≤\frac{16}{3}$
又∵0≤r≤7,∴r=5.
∴系数最大项为T6=${C}_{7}^{5}$x2•25y5=672x2y5.
故答案为:672x2y5.
点评 本题考查系数最大项,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
12.如图是某平面图形的直观图,则原平面图形的面积是( )
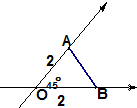

| A. | 4 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 8 |
9.若点(sinα,cosα)位于第四象限,则角α在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |