题目内容
2.已知点M(4,5)是⊙O:x2+y2-6x-8y=0内一点,则以点M为中点的圆O的弦长为( )| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{17}$ | C. | 2$\sqrt{23}$ | D. | 6 |
分析 化圆的方程为x2+y2-6x-8y=0为标准方程,求出圆心和半径,可得OM,即可求出以点M为中点的圆O的弦长.
解答 解:圆的方程为x2+y2-6x-8y=0化为(x-3)2+(y-4)2=25.
∴圆心O(3,4),半径为5,
∴OM=$\sqrt{2}$
∴以点M为中点的圆O的弦长为2$\sqrt{25-2}$=2$\sqrt{23}$.
故选:C.
点评 本题考查以点M为中点的圆O的弦长,考查直线与圆的方程的应用,圆的标准方程,是基础题.

练习册系列答案
相关题目
12.阅读下图所示的程序框图,该框图表示的函数是( )
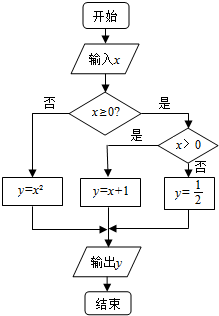

| A. | y=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{x+1,x<0}\end{array}\right.$ | B. | y=$\left\{\begin{array}{l}{\frac{1}{2},x≥0}\\{{x}^{2},x<0}\end{array}\right.$ | ||
| C. | y=$\left\{\begin{array}{l}{{x}^{2},x<0}\\{\frac{1}{2},x=0}\\{x+1,x>0}\end{array}\right.$ | D. | y=$\left\{\begin{array}{l}{{x}^{2},x>0}\\{\frac{1}{2},x=0}\\{x+1,x<0}\end{array}\right.$ |
7.盒中装有10个乒乓球,其中6个新球,4个旧球,不放回地依次取出2个球使用,在第一次取出新球的条件下,第二次也取到新球的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{1}{10}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{5}$ |
14.已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b=$\sqrt{3}$,A+C=2B,则sinC=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
12.如图是某平面图形的直观图,则原平面图形的面积是( )
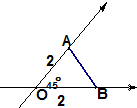

| A. | 4 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 8 |