题目内容
15．同时抛掷2枚硬币．（1）列出所有可能的结果；
（2）求恰有一枚为正面，一枚为反面的概率．
分析 （1）列举出抛掷2枚硬币的基本事件数即可；
（2）根据列举的基本事件数，计算对应的概率即可．
解答 解：（1）抛掷2枚硬币，
所有可能的结果是（正，正），（正，反），
（反，正），（反，反）共4种；…（4分）
（2）设抛掷2枚硬币，恰有一枚为正面，一枚为反面为事件A，
则事件A有（正，反），（反，正）2种结果 …（7分）
故P（A）=2424=1212． …（10分）
点评 本题考查了利用列举法求古典概型的概率问题，是基础题目．
练习册系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
相关题目
5．
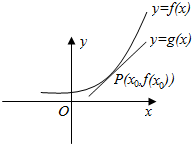已知可导函数y=f（x）在点P（x0，f（x0））处切线为l：y=g（x）（如图），设F（x）=f（x）-g（x），则（ ）
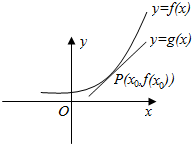已知可导函数y=f（x）在点P（x0，f（x0））处切线为l：y=g（x）（如图），设F（x）=f（x）-g（x），则（ ）| A． | F′（x0）=0，x=x0是F（x）的极大值点 | B． | F′（x0）=0，x=x0是F（x）的极小值点 | ||
| C． | F′（x0）≠0，x=x0不是F（x）的极值点 | D． | F′（x0）≠0，x=x0是F（x）的极值点 |
8．已知向量→a→a=（x，1），→b→b=（-x，x2），则向量→a→a+→b→b（ ）
| A． | 与向量→c→c=（0，1）垂直 | B． | 与向量→c→c=（0，1）平行 | ||
| C． | 与向量→d→d=（1，-1）垂直 | D． | 与向量→d→d=（1，-1）平行 |
5．函数y=√3−x√3−x+lg（x+1）的定义域是（ ）
| A． | （-1，3） | B． | [-1，3） | C． | （-1，3] | D． | （3，+∞） |