题目内容
已知数列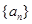 的前
的前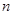 项和为
项和为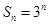 ,数列
,数列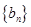 满足
满足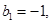
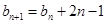 (
(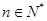 ).
).
(1)求数列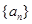 的通项公式;
的通项公式;
(2)求数列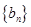 的通项公式;
的通项公式;
(3)求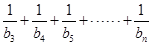 的值.
的值.
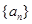 的前
的前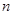 项和为
项和为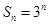 ,数列
,数列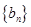 满足
满足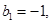
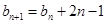 (
(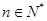 ).
).(1)求数列
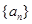 的通项公式;
的通项公式;(2)求数列
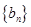 的通项公式;
的通项公式;(3)求
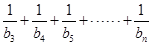 的值.
的值.(1) ;(2)
;(2) ;(3)
;(3) .
.
 ;(2)
;(2) ;(3)
;(3) .
.试题分析:(1)根据通项公式
 与前
与前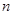 项和
项和 的关系式
的关系式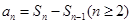 ,得到
,得到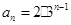
 ,注意检验
,注意检验 时,是否符合
时,是否符合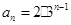 ,从而可写出数列
,从而可写出数列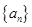 的通项公式;(2)根据
的通项公式;(2)根据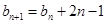 可得
可得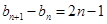 ,从而得到
,从而得到 ,将这些等式累加即可得到
,将这些等式累加即可得到 ,注意验证
,注意验证 时,是否符合
时,是否符合 ,从而又可得到数列
,从而又可得到数列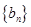 的通项公式;(3)由
的通项公式;(3)由 ,从而对
,从而对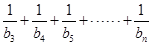 采用裂项相消法求和即可得到结果.
采用裂项相消法求和即可得到结果.试题解析:(1)
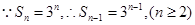


当
 时,
时,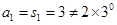 ,所
,所
(2)
 ,
,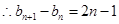
∴

以上各式相加得
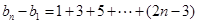

∵
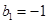 ,∴
,∴
(3)∵

∴
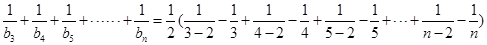
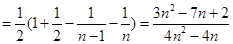 .
. 与前
与前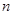 项和
项和 的关系式;2.累加法求通项;3.裂项相消法求和.
的关系式;2.累加法求通项;3.裂项相消法求和.
练习册系列答案
相关题目
 ,求证:
,求证: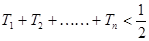 .
. 前
前 项和
项和 .
. 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变. ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;





 3
3

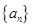 中,
中,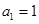 ,前
,前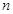 项的和是
项的和是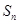 ,且
,且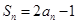 ,
,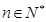 .
.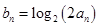 ,求
,求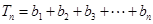 .
. 与
与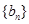 满足
满足 ,且
,且 ,设数列
,设数列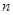 项和为
项和为 ,则
,则 =.
=.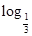 (Sn+1),求数列{bnan}的前n项和Tn.
(Sn+1),求数列{bnan}的前n项和Tn.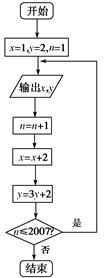
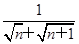 ,若{an}前n项和为24,则n为( ).
,若{an}前n项和为24,则n为( ).