题目内容
已知数列{an}的前n项和为Sn=3n-1.
(1)求数列{an}的通项公式;
(2)若bn=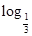 (Sn+1),求数列{bnan}的前n项和Tn.
(Sn+1),求数列{bnan}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)若bn=
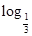 (Sn+1),求数列{bnan}的前n项和Tn.
(Sn+1),求数列{bnan}的前n项和Tn.(1)an=2×3n-1(2)-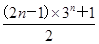 ,n∈N*
,n∈N*
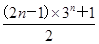 ,n∈N*
,n∈N*(1)当n=1时,a1=S1=2,
当n≥2时,an=Sn-Sn-1=(3n-1)-(3n-1-1)=2×3n-1,综上所述,an=2×3n-1.
(2)bn=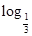 (Sn+1)=
(Sn+1)=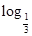 3n=-n,所以bnan=-2n×3n-1,
3n=-n,所以bnan=-2n×3n-1,
Tn=-2×1-4×31-6×32-…-2n×3n-1,
3Tn=-2×31-4×32-…-2(n-1)×3n-1-2n×3n,相减,得
-2Tn=-2×1-2×31-2×32-…-2×3n-1+2n×3n
=-2×(1+31+32+…+3n-1)+2n×3n,
所以Tn=(1+31+32+…+3n-1)-n×3n=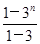 -n×3n=-
-n×3n=-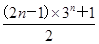 ,n∈N*
,n∈N*
当n≥2时,an=Sn-Sn-1=(3n-1)-(3n-1-1)=2×3n-1,综上所述,an=2×3n-1.
(2)bn=
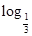 (Sn+1)=
(Sn+1)=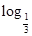 3n=-n,所以bnan=-2n×3n-1,
3n=-n,所以bnan=-2n×3n-1,Tn=-2×1-4×31-6×32-…-2n×3n-1,
3Tn=-2×31-4×32-…-2(n-1)×3n-1-2n×3n,相减,得
-2Tn=-2×1-2×31-2×32-…-2×3n-1+2n×3n
=-2×(1+31+32+…+3n-1)+2n×3n,
所以Tn=(1+31+32+…+3n-1)-n×3n=
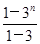 -n×3n=-
-n×3n=-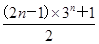 ,n∈N*
,n∈N*
练习册系列答案
相关题目
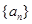 的前
的前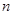 项和为
项和为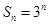 ,数列
,数列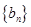 满足
满足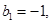
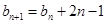 (
(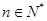 ).
).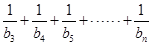 的值.
的值.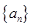 的前n项和为
的前n项和为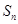 ,且
,且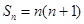 ,数列
,数列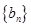 满足
满足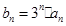 .
. 的前
的前 项和为
项和为 ,
, 是
是 与
与 的等比中项.
的等比中项. ,且
,且 ,求数列
,求数列 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前 .
.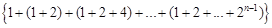 的前
的前 项和为_____________.
项和为_____________.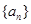 的前n项和为
的前n项和为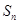 ,若
,若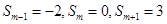 ,则
,则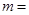 ( )
( ) 的前
的前 项和
项和 ,则此数列的通项公式为
,则此数列的通项公式为 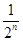 ,n∈N?,则a3=________.
,n∈N?,则a3=________. ,2
,2  ,3
,3  ,4
,4  ,…的前n项和为 .
,…的前n项和为 .