题目内容
(本题满分14分)离心率为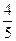 的椭圆
的椭圆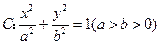 上有一点
上有一点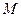 到椭圆两焦点的距离和为
到椭圆两焦点的距离和为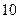 .以椭圆
.以椭圆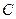 的右焦点
的右焦点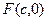 为圆心,短轴长为直径的圆有切线
为圆心,短轴长为直径的圆有切线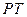 (
(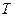 为切点),且点
为切点),且点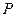 满足
满足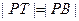 (
(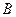 为椭圆
为椭圆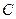 的上顶点)。(I)求椭圆的方程;(II)求点
的上顶点)。(I)求椭圆的方程;(II)求点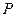 所在的直线方程
所在的直线方程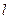 .
.
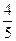 的椭圆
的椭圆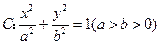 上有一点
上有一点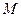 到椭圆两焦点的距离和为
到椭圆两焦点的距离和为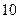 .以椭圆
.以椭圆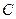 的右焦点
的右焦点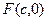 为圆心,短轴长为直径的圆有切线
为圆心,短轴长为直径的圆有切线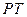 (
(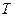 为切点),且点
为切点),且点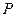 满足
满足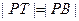 (
(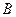 为椭圆
为椭圆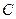 的上顶点)。(I)求椭圆的方程;(II)求点
的上顶点)。(I)求椭圆的方程;(II)求点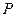 所在的直线方程
所在的直线方程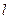 .
.(Ⅰ)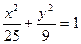 (Ⅱ)
(Ⅱ) 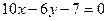
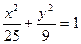 (Ⅱ)
(Ⅱ) 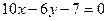
:(I)依题意有: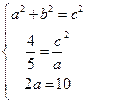 3分解得:
3分解得: 5分
5分
所以椭圆方程为: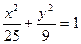 。6分
。6分
(II)设点 。由(I)得
。由(I)得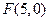 ,所以圆
,所以圆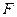 的方程为:
的方程为: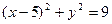 .……8分
.……8分
方法一(根轴法):把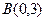 点当作圆
点当作圆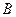 :
: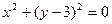 ,点
,点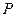 所在的直线是圆
所在的直线是圆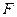 和圆
和圆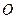 的根轴,所以
的根轴,所以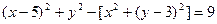 ,即
,即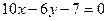 。
。
方法二(圆幂定理):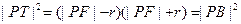 ,……10分
,……10分
 ,
,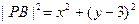 ,12分
,12分
所以 ,……13分化简得:
,……13分化简得: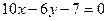 。………14分
。………14分
方法三(勾股定理):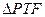 为直角三角形,所以
为直角三角形,所以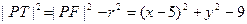 。又
。又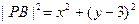 ,所以
,所以 ,化简得:
,化简得: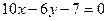 .
.
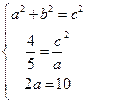 3分解得:
3分解得: 5分
5分所以椭圆方程为:
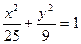 。6分
。6分(II)设点
 。由(I)得
。由(I)得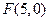 ,所以圆
,所以圆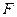 的方程为:
的方程为: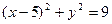 .……8分
.……8分方法一(根轴法):把
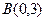 点当作圆
点当作圆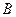 :
: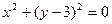 ,点
,点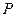 所在的直线是圆
所在的直线是圆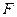 和圆
和圆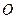 的根轴,所以
的根轴,所以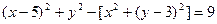 ,即
,即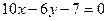 。
。方法二(圆幂定理):
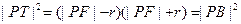 ,……10分
,……10分 ,
,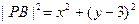 ,12分
,12分所以
 ,……13分化简得:
,……13分化简得: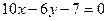 。………14分
。………14分方法三(勾股定理):
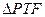 为直角三角形,所以
为直角三角形,所以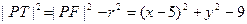 。又
。又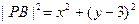 ,所以
,所以 ,化简得:
,化简得: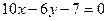 .
.
练习册系列答案
相关题目
 ,它的离心率为
,它的离心率为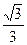 ,直线
,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.⑴求椭圆
的短半轴长为半径的圆相切.⑴求椭圆 ,左准线为
,左准线为 ,动直线
,动直线 垂直于直线
垂直于直线 ,线段
,线段 的垂直平分线交
的垂直平分线交 ,求动点
,求动点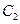 的方程;⑶将曲线
的方程;⑶将曲线 ,设曲线
,设曲线 ,焦点为
,焦点为 ,过
,过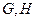 两点,过点
两点,过点 作平行于曲线
作平行于曲线 ,若
,若 ,试证明三点
,试证明三点 (
( 为坐标原点)在同一条直线上.
为坐标原点)在同一条直线上.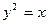
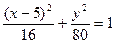
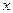
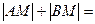
 相交于A、B两点,M是线段AB上的一点,
相交于A、B两点,M是线段AB上的一点,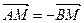 ,且点M在直线
,且点M在直线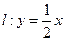 上.
上.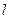 的对称点在单位圆
的对称点在单位圆 上,求椭圆的方程.
上,求椭圆的方程. 所表示的曲线是 ( )
所表示的曲线是 ( )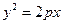 的焦点与椭圆
的焦点与椭圆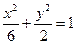 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )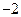
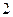


 :
: ,直线
,直线 交
交 两点,
两点, 是线段
是线段 的中点,过
的中点,过 轴的垂线交
轴的垂线交 .(1)证明:抛物线
.(1)证明:抛物线 使NA
使NA NB,若存在,求
NB,若存在,求
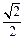 的椭圆,点F为其右焦点.
的椭圆,点F为其右焦点.
 ,
, 且有
且有 ,则
,则 点的轨迹是( )
点的轨迹是( )