题目内容
已知点 ,
, 且有
且有 ,则
,则 点的轨迹是( )
点的轨迹是( )
 ,
, 且有
且有 ,则
,则 点的轨迹是( )
点的轨迹是( )| A.椭圆 | B.双曲线 | C.线段 | D.两射线 |
C
∵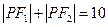 =
=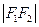 ,∴
,∴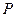 点在线段
点在线段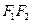 上,所以选
上,所以选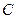
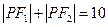 =
=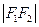 ,∴
,∴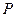 点在线段
点在线段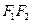 上,所以选
上,所以选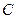

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
题目内容
 ,
, 且有
且有 ,则
,则 点的轨迹是( )
点的轨迹是( )| A.椭圆 | B.双曲线 | C.线段 | D.两射线 |
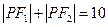 =
=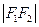 ,∴
,∴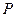 点在线段
点在线段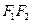 上,所以选
上,所以选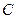

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案