题目内容
如图,已知圆O:x2+y2=2交x轴于A,B两点,点P(-1,1)为圆O上一点.曲线C是以AB为长轴,离心率为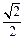 的椭圆,点F为其右焦点.
的椭圆,点F为其右焦点.

过原点O作直线PF的垂线交椭圆C的右准线l于点Q.
(1)求椭圆C的标准方程;(2)证明:直线PQ与圆O相切.
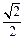 的椭圆,点F为其右焦点.
的椭圆,点F为其右焦点.
过原点O作直线PF的垂线交椭圆C的右准线l于点Q.
(1)求椭圆C的标准方程;(2)证明:直线PQ与圆O相切.
(Ⅰ) 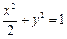 (Ⅱ)
(Ⅱ)
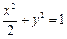 (Ⅱ)
(Ⅱ) (1)由题意,得a = ,e =
,e =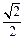 ,∴c =1,∴b2=1.
,∴c =1,∴b2=1.
所以椭圆C的标准方程为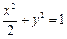 .… 6分
.… 6分
(2)∵P(-1,1),F(1,0),∴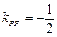 ,∴
,∴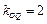 .所以直线OQ的方程为y =2x.10分
.所以直线OQ的方程为y =2x.10分
又椭圆的右准线方程为x =2,所以Q(2,4),所以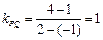 .
.
又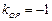 ,所以
,所以 ,即OP⊥PQ.故直线PQ与圆O相切.… 15分
,即OP⊥PQ.故直线PQ与圆O相切.… 15分
 ,e =
,e =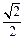 ,∴c =1,∴b2=1.
,∴c =1,∴b2=1.所以椭圆C的标准方程为
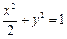 .… 6分
.… 6分(2)∵P(-1,1),F(1,0),∴
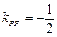 ,∴
,∴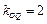 .所以直线OQ的方程为y =2x.10分
.所以直线OQ的方程为y =2x.10分又椭圆的右准线方程为x =2,所以Q(2,4),所以
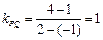 .
.又
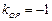 ,所以
,所以 ,即OP⊥PQ.故直线PQ与圆O相切.… 15分
,即OP⊥PQ.故直线PQ与圆O相切.… 15分
练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
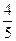 的椭圆
的椭圆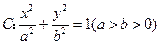 上有一点
上有一点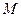 到椭圆两焦点的距离和为
到椭圆两焦点的距离和为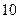 .以椭圆
.以椭圆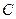 的右焦点
的右焦点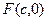 为圆心,短轴长为直径的圆有切线
为圆心,短轴长为直径的圆有切线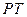 (
(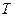 为切点),且点
为切点),且点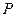 满足
满足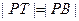 (
(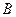 为椭圆
为椭圆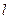 .
. 为直角坐标平面内x轴,y轴正方向上的单位向量.若向量
为直角坐标平面内x轴,y轴正方向上的单位向量.若向量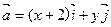 ,
,
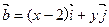 ,且
,且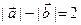 .(1)求满足上述条件的点
.(1)求满足上述条件的点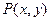 的轨迹方程;(2)设
的轨迹方程;(2)设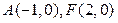 ,问是否存在常数
,问是否存在常数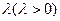 ,使得
,使得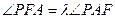 恒成立?证明你的结论.
恒成立?证明你的结论.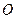 为坐标原点,给定两点
为坐标原点,给定两点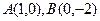 ,点
,点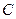 满足
满足 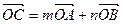 ,其中
,其中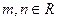 ,且
,且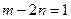 . (1)求点
. (1)求点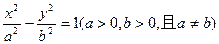 交于
交于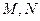 两点,且以
两点,且以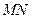 为直径的圆过原点,求证:
为直径的圆过原点,求证: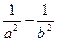 为定值;(3)在(2)的条件下,若双曲线的离心率不大于
为定值;(3)在(2)的条件下,若双曲线的离心率不大于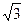 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.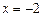 ,且直线l与x轴交于点M,圆
,且直线l与x轴交于点M,圆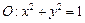 与x轴交于
与x轴交于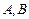 两点(如图).
两点(如图).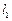 交圆于
交圆于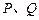 两点,且圆孤
两点,且圆孤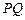 恰为圆周的
恰为圆周的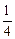 ,求直线
,求直线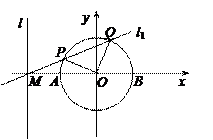
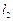 交(II)中的一个椭圆于
交(II)中的一个椭圆于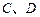 两点,其中
两点,其中 分)
分) 满足到点
满足到点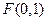 的距离比到直线
的距离比到直线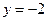 的距离小1.
的距离小1.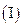 求曲线C的方程;
求曲线C的方程;
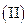 过点F的直线l与曲线C交于A、B两点.(
过点F的直线l与曲线C交于A、B两点.( ⅰ)过A、B两点分别作抛物线的切线,设其交点为M,证明
ⅰ)过A、B两点分别作抛物线的切线,设其交点为M,证明 :
: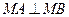 ;(ⅱ)是否在y轴上存在定点Q
;(ⅱ)是否在y轴上存在定点Q ,使得
,使得 无论AB怎样运动,都有
无论AB怎样运动,都有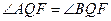 ?证明你的结论.
?证明你的结论.
 (Ⅰ)建立适当的坐标系,求双曲线E的方程;
(Ⅰ)建立适当的坐标系,求双曲线E的方程;
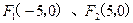 ,双曲线上一点P到两焦点的距离之差的绝对值等于6,求双曲线标准方程.
,双曲线上一点P到两焦点的距离之差的绝对值等于6,求双曲线标准方程.