题目内容
已知抛物线 :
: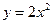 ,直线
,直线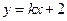 交
交 于
于 两点,
两点, 是线段
是线段 的中点,过
的中点,过 作
作 轴的垂线交
轴的垂线交 于点
于点 .(1)证明:抛物线
.(1)证明:抛物线 在点
在点 处的切线与
处的切线与 平行;(2)是否存在实数
平行;(2)是否存在实数 使NA
使NA NB,若存在,求
NB,若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
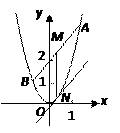
 :
: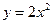 ,直线
,直线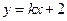 交
交 于
于 两点,
两点, 是线段
是线段 的中点,过
的中点,过 作
作 轴的垂线交
轴的垂线交 于点
于点 .(1)证明:抛物线
.(1)证明:抛物线 在点
在点 处的切线与
处的切线与 平行;(2)是否存在实数
平行;(2)是否存在实数 使NA
使NA NB,若存在,求
NB,若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.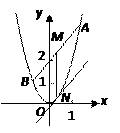
(Ⅰ) 略 (Ⅱ) 

法一:(Ⅰ)如图,设 ,
,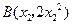 ,把
,把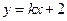 代入
代入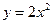 得
得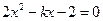 ,由韦达定理得
,由韦达定理得 ,
, ,
,

 ,
,
 点的坐标为
点的坐标为 .
.
设抛物线在点 处的切线
处的切线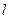 的方程为
的方程为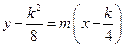 ,
,
将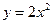 代入上式得
代入上式得 ,
, 直线
直线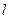 与抛物线
与抛物线 相切,
相切,
 ,
, .即
.即 .
.
(Ⅱ)假设存在实数 ,使
,使 ,则
,则 ,又
,又 是
是 的中点,
的中点,
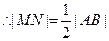 .由(Ⅰ)知
.由(Ⅰ)知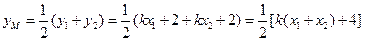
 .
.
 轴,
轴,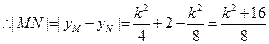 .
.
又
. ,解得
,解得 .即存在
.即存在 ,使
,使 .
.
解法二:(Ⅰ)如图,设 ,把
,把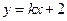 代入
代入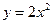 得
得
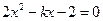 .由韦达定理得
.由韦达定理得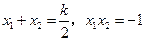 .
.

 ,
,
 点的坐标为
点的坐标为 .
. ,
, ,
,
 抛物线在点
抛物线在点 处的切线
处的切线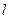 的斜率为
的斜率为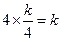 ,
,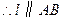 .
.
(Ⅱ)假设存在实数 ,使
,使 .
.
由(Ⅰ)知 ,则
,则




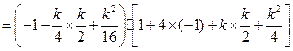

 ,
, ,
, ,解得
,解得 .即存在
.即存在 ,使
,使 .
.
 ,
,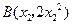 ,把
,把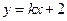 代入
代入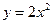 得
得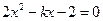 ,由韦达定理得
,由韦达定理得 ,
, ,
,
 ,
,
 点的坐标为
点的坐标为 .
.设抛物线在点
 处的切线
处的切线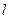 的方程为
的方程为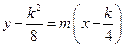 ,
,将
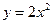 代入上式得
代入上式得 ,
, 直线
直线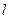 与抛物线
与抛物线 相切,
相切, ,
, .即
.即 .
.(Ⅱ)假设存在实数
 ,使
,使 ,则
,则 ,又
,又 是
是 的中点,
的中点,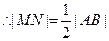 .由(Ⅰ)知
.由(Ⅰ)知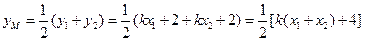
 .
.
 轴,
轴,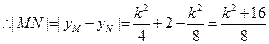 .
.又

.
 ,解得
,解得 .即存在
.即存在 ,使
,使 .
.解法二:(Ⅰ)如图,设
 ,把
,把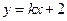 代入
代入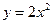 得
得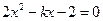 .由韦达定理得
.由韦达定理得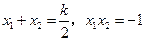 .
.
 ,
,
 点的坐标为
点的坐标为 .
. ,
, ,
, 抛物线在点
抛物线在点 处的切线
处的切线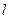 的斜率为
的斜率为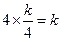 ,
, .
.(Ⅱ)假设存在实数
 ,使
,使 .
.由(Ⅰ)知
 ,则
,则



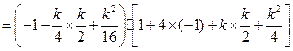

 ,
, ,
, ,解得
,解得 .即存在
.即存在 ,使
,使 .
.
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
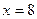
 的椭圆
的椭圆 上有一点
上有一点 到椭圆两焦点的距离和为
到椭圆两焦点的距离和为 .以椭圆
.以椭圆 的右焦点
的右焦点 为圆心,短轴长为直径的圆有切线
为圆心,短轴长为直径的圆有切线 (
( 为切点),且点
为切点),且点 满足
满足 (
( 为椭圆
为椭圆 .
. 与双曲线
与双曲线 的左支交于
的左支交于 两点,另一直线
两点,另一直线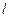 过点
过点 和
和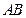 的中点,求直线
的中点,求直线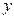 轴上的截距
轴上的截距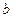 的取值范围。
的取值范围。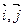 为直角坐标平面内x轴,y轴正方向上的单位向量.若向量
为直角坐标平面内x轴,y轴正方向上的单位向量.若向量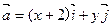 ,
,
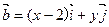 ,且
,且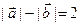 .(1)求满足上述条件的点
.(1)求满足上述条件的点 的轨迹方程;(2)设
的轨迹方程;(2)设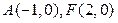 ,问是否存在常数
,问是否存在常数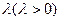 ,使得
,使得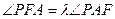 恒成立?证明你的结论.
恒成立?证明你的结论.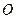 为坐标原点,给定两点
为坐标原点,给定两点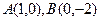 ,点
,点 满足
满足  ,其中
,其中 ,且
,且 . (1)求点
. (1)求点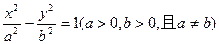 交于
交于 两点,且以
两点,且以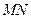 为直径的圆过原点,求证:
为直径的圆过原点,求证: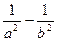 为定值;(3)在(2)的条件下,若双曲线的离心率不大于
为定值;(3)在(2)的条件下,若双曲线的离心率不大于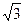 ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围. 分)
分) 满足到点
满足到点 的距离比到直线
的距离比到直线 的距离小1.
的距离小1. 求曲线C的方程;
求曲线C的方程;
 过点F的直线l与曲线C交于A、B两点.(
过点F的直线l与曲线C交于A、B两点.( ⅰ)过A、B两点分别作抛物线的切线,设其交点为M,证明
ⅰ)过A、B两点分别作抛物线的切线,设其交点为M,证明 :
: ;(ⅱ)是否在y轴上存在定点Q
;(ⅱ)是否在y轴上存在定点Q ,使得
,使得 无论AB怎样运动,都有
无论AB怎样运动,都有 ?证明你的结论.
?证明你的结论.