题目内容
(本小题满分14分)已知椭圆 ,它的离心率为
,它的离心率为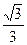 ,直线
,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.⑴求椭圆
的短半轴长为半径的圆相切.⑴求椭圆 的方程;⑵设椭圆
的方程;⑵设椭圆 的左焦点为
的左焦点为 ,左准线为
,左准线为 ,动直线
,动直线 垂直于直线
垂直于直线 ,垂足为点
,垂足为点 ,线段
,线段 的垂直平分线交
的垂直平分线交 于点
于点 ,求动点
,求动点 的轨迹
的轨迹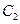 的方程;⑶将曲线
的方程;⑶将曲线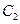 向右平移2个单位得到曲线
向右平移2个单位得到曲线 ,设曲线
,设曲线 的准线为
的准线为 ,焦点为
,焦点为 ,过
,过 作直线
作直线 交曲线
交曲线 于
于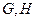 两点,过点
两点,过点 作平行于曲线
作平行于曲线 的对称轴的直线
的对称轴的直线 ,若
,若 ,试证明三点
,试证明三点 (
( 为坐标原点)在同一条直线上.
为坐标原点)在同一条直线上.
 ,它的离心率为
,它的离心率为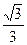 ,直线
,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.⑴求椭圆
的短半轴长为半径的圆相切.⑴求椭圆 的方程;⑵设椭圆
的方程;⑵设椭圆 的左焦点为
的左焦点为 ,左准线为
,左准线为 ,动直线
,动直线 垂直于直线
垂直于直线 ,垂足为点
,垂足为点 ,线段
,线段 的垂直平分线交
的垂直平分线交 于点
于点 ,求动点
,求动点 的轨迹
的轨迹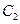 的方程;⑶将曲线
的方程;⑶将曲线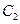 向右平移2个单位得到曲线
向右平移2个单位得到曲线 ,设曲线
,设曲线 的准线为
的准线为 ,焦点为
,焦点为 ,过
,过 作直线
作直线 交曲线
交曲线 于
于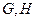 两点,过点
两点,过点 作平行于曲线
作平行于曲线 的对称轴的直线
的对称轴的直线 ,若
,若 ,试证明三点
,试证明三点 (
( 为坐标原点)在同一条直线上.
为坐标原点)在同一条直线上.(Ⅰ)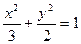 (Ⅱ)
(Ⅱ) 三点共线
三点共线
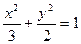 (Ⅱ)
(Ⅱ) 三点共线
三点共线(Ⅰ)由题意可得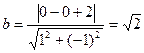 , (2分)
, (2分)
由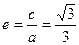 ,得
,得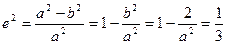 ,∴
,∴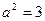 , (4分)
, (4分)
∴椭圆 的方程为
的方程为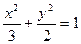 .
.  (4分)
(4分)
(Ⅱ)由(Ⅰ)可得椭圆 的左焦点为
的左焦点为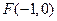 ,左准线为
,左准线为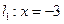 ,
,
连结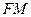 ,则
,则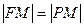 ,设
,设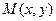 ,则
,则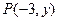 ,
,
∴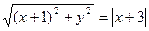 ,(6分)化简得
,(6分)化简得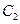 的方程为
的方程为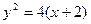 .(8分)
.(8分)
(Ⅲ)将曲线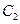 向右平移2个单位,得曲线
向右平移2个单位,得曲线 的方程为:
的方程为: 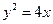 ,其焦点为
,其焦点为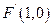 ,
,
准线为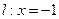 ,对称轴为
,对称轴为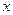 轴.
轴. (10分)
(10分)
设直线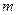 的方程为
的方程为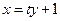 ,代入y2=4x,得y2-4ty-4=0.
,代入y2=4x,得y2-4ty-4=0.
由题意,可设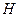 (
(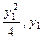 ),
), (
(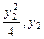 ),则y1y2=-4,
),则y1y2=-4,
且有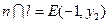 (12分)∴
(12分)∴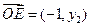 ,
,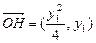 ,
,
得 .∴
.∴ 三点共线. (14分)
三点共线. (14分)
评析:证明三点共线的方法很多,这里运用向量共线定理来证,体现了平面向量与解析几何知识的交汇和平面向量知识在解析几何中的应用.近几年的高考突出了在知识网络的交汇点处设计命题的要求,平面向量与解析几何知识的综合考查成为一个不衰的热点,复习中要引起重视.
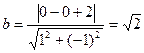 , (2分)
, (2分)由
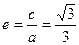 ,得
,得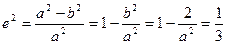 ,∴
,∴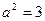 , (4分)
, (4分)∴椭圆
 的方程为
的方程为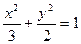 .
.  (4分)
(4分)(Ⅱ)由(Ⅰ)可得椭圆
 的左焦点为
的左焦点为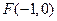 ,左准线为
,左准线为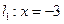 ,
, 连结
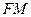 ,则
,则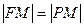 ,设
,设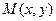 ,则
,则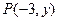 ,
,∴
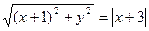 ,(6分)化简得
,(6分)化简得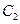 的方程为
的方程为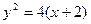 .(8分)
.(8分)(Ⅲ)将曲线
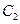 向右平移2个单位,得曲线
向右平移2个单位,得曲线 的方程为:
的方程为: 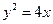 ,其焦点为
,其焦点为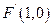 ,
,准线为
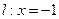 ,对称轴为
,对称轴为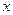 轴.
轴. (10分)
(10分)设直线
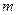 的方程为
的方程为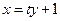 ,代入y2=4x,得y2-4ty-4=0.
,代入y2=4x,得y2-4ty-4=0.由题意,可设
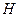 (
(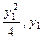 ),
), (
(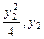 ),则y1y2=-4,
),则y1y2=-4,且有
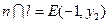 (12分)∴
(12分)∴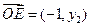 ,
,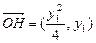 ,
,得
 .∴
.∴ 三点共线. (14分)
三点共线. (14分)评析:证明三点共线的方法很多,这里运用向量共线定理来证,体现了平面向量与解析几何知识的交汇和平面向量知识在解析几何中的应用.近几年的高考突出了在知识网络的交汇点处设计命题的要求,平面向量与解析几何知识的综合考查成为一个不衰的热点,复习中要引起重视.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
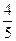 的椭圆
的椭圆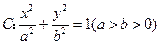 上有一点
上有一点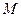 到椭圆两焦点的距离和为
到椭圆两焦点的距离和为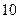 .以椭圆
.以椭圆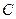 的右焦点
的右焦点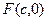 为圆心,短轴长为直径的圆有切线
为圆心,短轴长为直径的圆有切线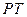 (
(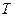 为切点),且点
为切点),且点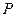 满足
满足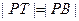 (
(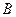 为椭圆
为椭圆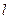 .
. 分)
分) 满足到点
满足到点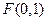 的距离比到直线
的距离比到直线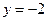 的距离小1.
的距离小1. 求曲线C的方程;
求曲线C的方程;
 过点F的直线l与曲线C交于A、B两点.(
过点F的直线l与曲线C交于A、B两点.( ⅰ)过A、B两点分别作抛物线的切线,设其交点为M,证明
ⅰ)过A、B两点分别作抛物线的切线,设其交点为M,证明 :
: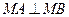 ;(ⅱ)是否在y轴上存在定点Q
;(ⅱ)是否在y轴上存在定点Q ,使得
,使得 无论AB怎样运动,都有
无论AB怎样运动,都有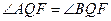 ?证明你的结论.
?证明你的结论.
 (Ⅰ)建立适当的坐标系,求双曲线E的方程;
(Ⅰ)建立适当的坐标系,求双曲线E的方程;
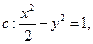 设过点
设过点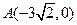 的直线l的方向向量
的直线l的方向向量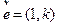
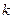 >
>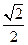 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为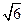 .
. :
: 上一点
上一点 到其焦点的距离为
到其焦点的距离为 .
. 与
与 的值;
的值; 的横坐标为
的横坐标为 ,过
,过 ,交
,交 轴于点
轴于点 ,过点
,过点 的垂线交
的垂线交 .若
.若 是
是 的最小值.
的最小值.