题目内容
16．tan10°tan20°+$\sqrt{3}$（tan10°+tan20°）=（ ）| A． | -1 | B． | $\sqrt{3}$ | C． | 1 | D． | -$\sqrt{3}$ |
分析 把题中的tan10°+tan20°换成tan30°（1-tan10°tan20°），化简可得所给式子的值．
解答 解：tan10°tan20°+$\sqrt{3}（tan{10^0}+tan{20^0}）$=tan10°tan20°+$\sqrt{3}$•tan30°（1-tan10°tan20°）
=tan10°tan20°+1-tan10°tan20°=1，
故选：C．
点评 本题主要考查两家和的正切公式的应用，属于基础题．
练习册系列答案
相关题目
15．
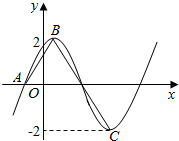已知函数$f（x）=2sin（ωx+φ）（ω＞0，|φ|＜\frac{π}{2}）$的部分图象如图所示，A、B、C分别是函数图象与x轴交点、图象的最高点、图象的最低点．若f（0）=$\sqrt{3}$，
且$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\frac{{π}^{2}}{8}$-8．则f（x）的解析式为（ ）
已知函数$f（x）=2sin（ωx+φ）（ω＞0，|φ|＜\frac{π}{2}）$的部分图象如图所示，A、B、C分别是函数图象与x轴交点、图象的最高点、图象的最低点．若f（0）=$\sqrt{3}$，且$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\frac{{π}^{2}}{8}$-8．则f（x）的解析式为（ ）
| A． | f（x）=2sin（2x+$\frac{π}{3}$） | B． | f（x）=2sin（2x+$\frac{π}{6}$） | C． | f（x）=2sin（3x+$\frac{π}{3}$） | D． | f（x）=2sin（3x+$\frac{π}{6}$） |
4．已知数列{an}的通项${a_n}=\left\{\begin{array}{l}{（-2）^n}\;\;\;\;\;\;n为奇数\\ n\;\;\;\;\;\;\;\;\;\;\;\;n为偶数\end{array}\right.$，则a4•a3=（ ）
| A． | 12 | B． | 32 | C． | -32 | D． | 48 |
8．人将一枚硬币连掷了3次，正面朝上的情形出现了2次，若用A表示这一事件，则A的（ ）
| A． | 概率为$\frac{2}{3}$ | B． | 概率为$\frac{1}{3}$ | C． | 概率为$\frac{1}{4}$ | D． | 概率$\frac{3}{8}$ |
5．某小区有老年人28个，中年人57个，年轻人63个，为了调查他们的身体健康状况，从他们中抽取容量为21的样本，最适合抽取样本的方法是（ ）
| A． | 简单随机抽样 | |
| B． | 系统抽样 | |
| C． | 分层抽样 | |
| D． | 先从中年人中随机剔除1人，再用分层抽样 |