题目内容
7.已知函数f(x)=x-$\frac{a}{x}$+b(2-lnx)在x=1处的切线的斜率为零.(Ⅰ)试用含a的代数式表示b;
(Ⅱ)若函数f(x)在区间[2,3]上单调递增,求实数a的取值范围;
(Ⅲ)是否存在实数a,使得函数y=f(x)图象与直线y=2a有两个交点?若存在,求出所有a的值;若不存在,请说明理由.
分析 (Ⅰ),先求导,再根据导数的几何意义,由已知得f'(1)=0,代入即可求出b=a+1;
(Ⅱ)先求导,再分离参数,得到即a≤x在区间[2,3]上恒成立,求出最小值即可;
(Ⅲ)f(x)-2a=0,有两个根,构造函数g(x)=x-$\frac{a}{x}$+(a+1)lnx+2,求导,分类讨论函数的单调性,根据零点存在定理,即可判断.
解答 解:(I)∵$f'(x)=1+\frac{a}{x^2}-\frac{b}{x}$(x>0),…(1分)
由已知得f'(1)=0,
∴b=a+1.…(2分)
(II)由(I)得$f'(x)=\frac{(x-a)(x-1)}{x^2}$.
要使函数f(x)在区间[2,3]上单调递增,
即要使$f'(x)=\frac{(x-a)(x-1)}{x^2}≥0$在区间[2,3]上恒成立.…(4分)
即x-a≥0在区间[2,3]上恒成立,∴a≤xmin(x∈[2,3]),∴a≤2.…(6分)
(Ⅲ)由f(x)=2a得$x-\frac{a}{x}-(a+1)lnx+2=0$有两个实根
令$g(x)=x-\frac{a}{x}-(a+1)lnx+2$则$g'(x)=\frac{(x-a)(x-1)}{x^2}$,…(7分)
(1)当a≤0时,函数y=g(x)在(0,1)上是减函数,在(1,+∞)是增函数,g(x)min=g(1)=3-a>0
此时函数y=g(x)无零点,不合题意;…(8分)
(2)当a=1时,$g'(x)={\frac{(x-1)}{x^2}^2}≥0$,
∴函数y=g(x)在(0,+∞)是增函数,不合题意;…(9分)
(3)当0<a<1时,函数y=g(x)在(0,a),(1,+∞)上是增函数;在(a,1)上是减函数,
∵g(1)=3-a≠0
要使函数g(x)有两个零点则只需g(a)=0解得a=e不合题意;…(10分)
(4)当a>1时,函数y=g(x)在(0,1),(a,+∞)上是增函数;在(1,a)上是减函数
要使函数g(x)有两个零点则只需g(a)=0或g(1)=0解得a=e或a=3
综上所述,a=e或a=3.…(12分)
点评 本题主要考查函数与导数等基础知识,考查运算求解能力、推理论证能力,考查分类与整合思想、数形结合思想、函数与方程思想及化归思想,属于难题.

| A. | (1,1) | B. | (2,2) | C. | (2,1) | D. | (2,0) |
| A. | B⊆A | B. | A⊆B | C. | A=B | D. | A∩B=Φ |
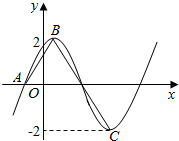 已知函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,A、B、C分别是函数图象与x轴交点、图象的最高点、图象的最低点.若f(0)=$\sqrt{3}$,
已知函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,A、B、C分别是函数图象与x轴交点、图象的最高点、图象的最低点.若f(0)=$\sqrt{3}$,且$\overrightarrow{AB}$•$\overrightarrow{BC}$=$\frac{{π}^{2}}{8}$-8.则f(x)的解析式为( )
| A. | f(x)=2sin(2x+$\frac{π}{3}$) | B. | f(x)=2sin(2x+$\frac{π}{6}$) | C. | f(x)=2sin(3x+$\frac{π}{3}$) | D. | f(x)=2sin(3x+$\frac{π}{6}$) |
| A. | $\frac{\sqrt{3}}{3}$ | B. | 1 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
| A. | 概率为$\frac{2}{3}$ | B. | 概率为$\frac{1}{3}$ | C. | 概率为$\frac{1}{4}$ | D. | 概率$\frac{3}{8}$ |