题目内容
【题目】已知:f(x)=lg(ax﹣bx)(a>1>b>0).
(1)求f(x)的定义域;
(2)判断f(x)在其定义域内的单调性.
【答案】
(1)解:要使函数有意义,则ax﹣bx>0,∴ ,
∵ ,∴x>0,∴f(x)的定义域为(0,+∞).
(2)解:设x2>x1>0,∵a>1>b>0,
∴ , ,则 ,
∴ ,∴ 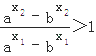 .
.
∵函数y=lgx在定义域上是增函数,
∴f(x2)﹣f(x1)>0,即f(x2)>f(x1),
∴f(x)在(0,+∞)是增函数.
【解析】(1)由对数的真数大于零得,ax﹣bx>0,再由a>1>b>0和指数函数的性质,求出不等式解集即函数的定义域;(2)先在定义域任取两个自变量,即x2>x1>0,利用指数函数的性质比较对应真数的大小,再根据y=lgx在定义域上是增函数,得出f(x2)与f(x1)的大小,判断出此函数的单调性;
【考点精析】本题主要考查了函数单调性的性质的相关知识点,需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集才能正确解答此题.

练习册系列答案
相关题目