题目内容
已知函数f(x)=sin(2x- ),若存在a∈(0,π),使得f(x+a)=f(x-a)恒成立,则a的值是( )
),若存在a∈(0,π),使得f(x+a)=f(x-a)恒成立,则a的值是( )
 ),若存在a∈(0,π),使得f(x+a)=f(x-a)恒成立,则a的值是( )
),若存在a∈(0,π),使得f(x+a)=f(x-a)恒成立,则a的值是( )A. | B. | C.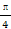 | D. |
D
因为函数满足f(x+a)=f(x-a),所以函数是周期函数,且周期为2a,又a∈(0,π),所以2a=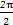 ,所以a=
,所以a=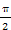 .
.
【方法技巧】周期函数的理解
(1)周期函数定义中的等式:f(x+T)=f(x)是定义域内的恒等式,即对定义域内的每个x值都成立,若只是存在个别x满足等式的常数T不是周期.
(2)每个周期函数的定义域是一个无限集,其周期有无穷多个,对于周期函数y=f(x),T是周期,则kT(k∈Z,k≠0)也是周期,但并非所有周期函数都有最小正周期.
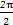 ,所以a=
,所以a=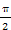 .
.【方法技巧】周期函数的理解
(1)周期函数定义中的等式:f(x+T)=f(x)是定义域内的恒等式,即对定义域内的每个x值都成立,若只是存在个别x满足等式的常数T不是周期.
(2)每个周期函数的定义域是一个无限集,其周期有无穷多个,对于周期函数y=f(x),T是周期,则kT(k∈Z,k≠0)也是周期,但并非所有周期函数都有最小正周期.

练习册系列答案
相关题目
 .
. 时,求函数
时,求函数 的单调递增区间;
的单调递增区间; 的内角
的内角 的对应边分别为
的对应边分别为 ,且
,且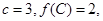 若向量
若向量 与向量
与向量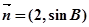 共线,求
共线,求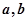 的值.
的值. 对称,则函数的解析式为________________.
对称,则函数的解析式为________________.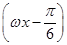 +1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为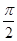 .
.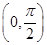 ,f
,f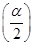 =2,求α的值.
=2,求α的值.
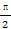 ,1).
,1).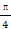 )=
)=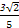 且α∈(0,
且α∈(0,



 对称,则|φ|的最小值是( )
对称,则|φ|的最小值是( )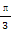


 cos ωx(x∈R,ω>0)满足f(α)=-2,f(β)=0,且|α-β|的最小值为
cos ωx(x∈R,ω>0)满足f(α)=-2,f(β)=0,且|α-β|的最小值为 ,则函数f(x)的单调递增区间为________.
,则函数f(x)的单调递增区间为________.