题目内容
如图,在直角梯形ABCD中,AD//BC,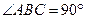 ,当E、F分别在线段AD、BC上,且
,当E、F分别在线段AD、BC上,且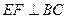 ,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
小题1:判断直线AD与BC是否共面,并证明你的结论;
小题2:当直线AC与平面EFCD所成角为多少时,二面角A—DC—E的大小是60°。

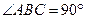 ,当E、F分别在线段AD、BC上,且
,当E、F分别在线段AD、BC上,且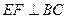 ,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。小题1:判断直线AD与BC是否共面,并证明你的结论;
小题2:当直线AC与平面EFCD所成角为多少时,二面角A—DC—E的大小是60°。

解:
小题1: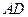 、
、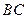 是异面直线, (1分)
是异面直线, (1分)
法一(反证法)假设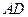 、
、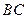 共面为
共面为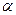 .
.
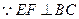 ,
,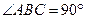 ,
,
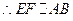 ,
, ,
,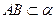 .
.
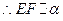 ,又
,又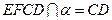
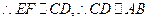 .
.
这与 为梯形矛盾.故假设不成立.
为梯形矛盾.故假设不成立.
即 、
、 是异面直线. (5分)
是异面直线. (5分)
法二:在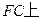 取一点M,使
取一点M,使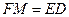 ,又
,又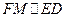 ,
,
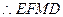 是平行四边形.
是平行四边形.
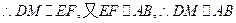 ,
,
则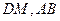 确定平面
确定平面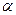 ,
,
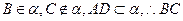 与
与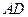 是异面直线.
是异面直线.
小题2:法一:延长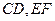 ,相交于N,AE=2,AD=4,BC=6,
,相交于N,AE=2,AD=4,BC=6,
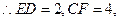 设
设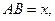
则△NDE中,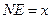 ,
,
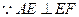 ,平面
,平面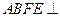 平面
平面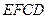 ,
,
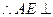 平面
平面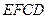 .
.
过E作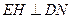 于H,连结AH,
于H,连结AH,
则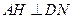 .
.
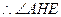 是二面角
是二面角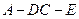 的平面角,
的平面角,
则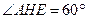 . (8分)
. (8分)
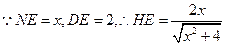 ,
,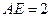 ,
,
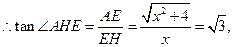
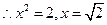 ,
,
此时在△EFC中,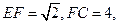
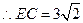 . (10分)
. (10分)
又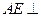 平面
平面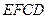 ,
,
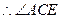 是直线
是直线 与平面
与平面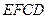 所成的角,
所成的角,
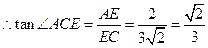 . (12分)
. (12分)
即当直线 与平面
与平面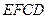 所成角为
所成角为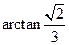 时,
时,
二面角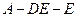 的大小为
的大小为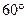 。
。
法二: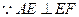 ,面
,面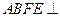 面
面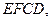
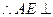 平面
平面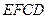 .
.
又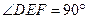 .
.
故可以以E为原点,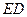 为x轴,
为x轴,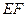 为
为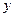 轴,
轴,
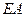 为Z轴建立空间直角坐标系,
为Z轴建立空间直角坐标系,
可求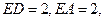 设
设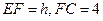 .
.
则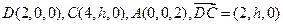 ,
,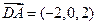 ,
,
得平面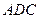 的法向量
的法向量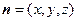 ,
,
则有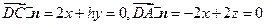 ,
,
可取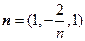 .
.
平面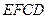 的法向量
的法向量
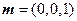 .
.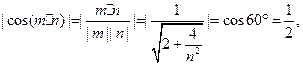
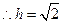 .(8分)
.(8分)
此时,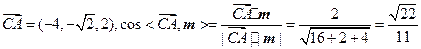 .
.
设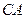 与平面
与平面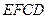 所成角为
所成角为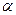 ,
,
则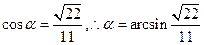 .
.
即当直线AC与平面EFCD所成角的大小为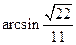 时,
时,
二面角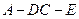 的大小为
的大小为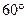 .(12分)
.(12分)
小题1:
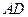 、
、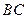 是异面直线, (1分)
是异面直线, (1分)法一(反证法)假设
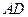 、
、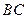 共面为
共面为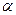 .
.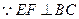 ,
,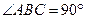 ,
,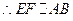 ,
, ,
,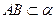 .
.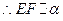 ,又
,又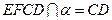
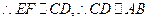 .
.这与
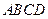 为梯形矛盾.故假设不成立.
为梯形矛盾.故假设不成立.即
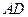 、
、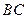 是异面直线. (5分)
是异面直线. (5分)法二:在
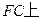 取一点M,使
取一点M,使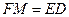 ,又
,又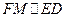 ,
, 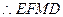 是平行四边形.
是平行四边形.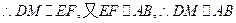 ,
,则
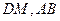 确定平面
确定平面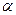 ,
,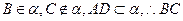 与
与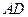 是异面直线.
是异面直线.小题2:法一:延长
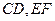 ,相交于N,AE=2,AD=4,BC=6,
,相交于N,AE=2,AD=4,BC=6, 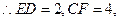 设
设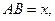
则△NDE中,
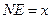 ,
,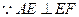 ,平面
,平面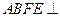 平面
平面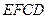 ,
,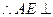 平面
平面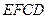 .
.过E作
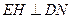 于H,连结AH,
于H,连结AH,则
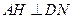 .
.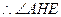 是二面角
是二面角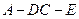 的平面角,
的平面角,则
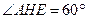 . (8分)
. (8分)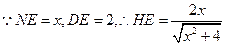 ,
,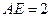 ,
,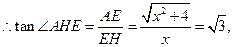
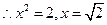 ,
,此时在△EFC中,
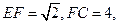
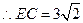 . (10分)
. (10分)又
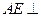 平面
平面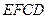 ,
,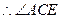 是直线
是直线 与平面
与平面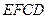 所成的角,
所成的角,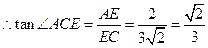 . (12分)
. (12分)即当直线
 与平面
与平面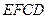 所成角为
所成角为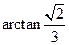 时,
时,二面角
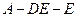 的大小为
的大小为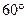 。
。法二:
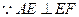 ,面
,面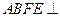 面
面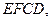
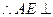 平面
平面 .
.又
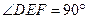 .
.故可以以E为原点,
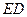 为x轴,
为x轴,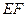 为
为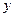 轴,
轴,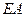 为Z轴建立空间直角坐标系,
为Z轴建立空间直角坐标系,可求
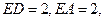 设
设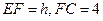 .
.则
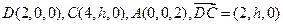 ,
,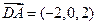 ,
,得平面
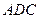 的法向量
的法向量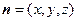 ,
,则有
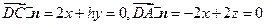 ,
,可取
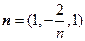 .
.平面
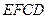 的法向量
的法向量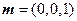 .
.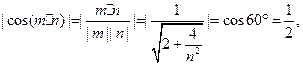
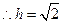 .(8分)
.(8分)此时,
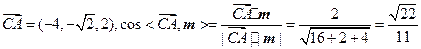 .
.设
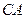 与平面
与平面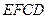 所成角为
所成角为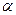 ,
,则
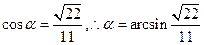 .
.即当直线AC与平面EFCD所成角的大小为
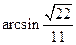 时,
时,二面角
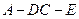 的大小为
的大小为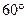 .(12分)
.(12分)略

练习册系列答案
相关题目
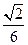 ,求圆锥的体积.
,求圆锥的体积.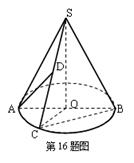
 为AB中点,F为PC中点.
为AB中点,F为PC中点.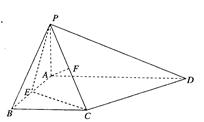
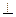 底面ABCD,PA=2,
底面ABCD,PA=2,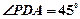 ,
,
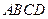 中,
中,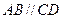 ,
,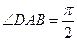 ,点
,点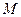 、
、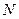 分别在
分别在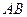 ,
,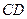 上,且
上,且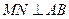 ,
,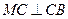 ,
,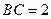 ,
,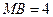 ,现将梯形
,现将梯形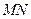 折起,使平面
折起,使平面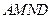 与平面
与平面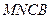 垂直(如图乙).
垂直(如图乙).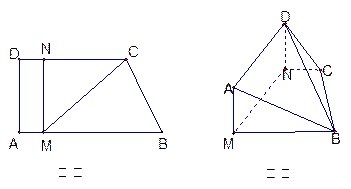
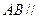 平面
平面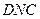 ;
;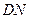 的长为何值时,
的长为何值时,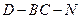 的大小为
的大小为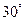 ?
?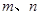 是两条不同的直线,
是两条不同的直线,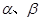 是两个不同的平面,有下列命题:
是两个不同的平面,有下列命题: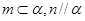 ,则
,则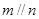 ; ②若
; ②若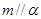 ,
,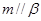 ,则
,则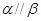 ;
;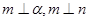 ,则
,则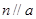 ; ④若
; ④若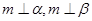 ,则
,则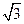 ,则其外接球的表面积是 。
,则其外接球的表面积是 。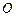 的半径为1,
的半径为1,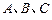 三点都在球面上,且每两点间的球面距离均为
三点都在球面上,且每两点间的球面距离均为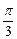 ,则球心
,则球心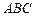 的距离为
的距离为 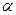 、
、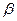 、
、 为三个互不重合的平面,对于下列命题:
为三个互不重合的平面,对于下列命题: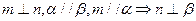 ②
②
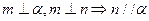 ④若m、n与
④若m、n与 .4
.4