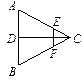题目内容
(本小题共13分)
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,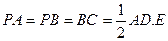 为AB中点,F为PC中点.
为AB中点,F为PC中点.
(I)求证:PE⊥BC;
(II)求二面角C—PE—A的余弦值;
(III)若四棱锥P—ABCD的体积为4,求AF的长.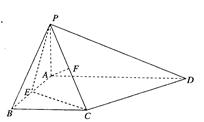
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=
∠BAD=90°,
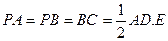 为AB中点,F为PC中点.
为AB中点,F为PC中点.(I)求证:PE⊥BC;
(II)求二面角C—PE—A的余弦值;
(III)若四棱锥P—ABCD的体积为4,求AF的长.

(I)证明见解析。
(II)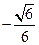
(III)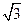
(II)
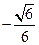
(III)
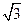
(I)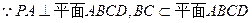
∴PA⊥BC
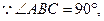
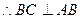
∴BC⊥平面PAB
又E是AB中点,
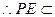 平面PAB
平面PAB
∴BC⊥PE. …………6分
(II)建立直角坐标系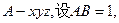
则B(1,0,0),C(1,1,0),P(0,0,1),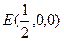
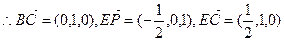
由(I)知,BC⊥平面PAE,
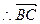 是平面PAE的法向量.
是平面PAE的法向量.
设平面PEC的法向量为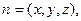
则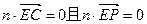
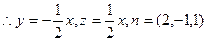
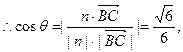
二面角C—PE—A的余弦值为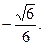 …………10分
…………10分
(III)连结BC,设AB=a,
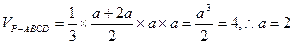
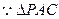 是直角三角形,
是直角三角形,
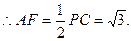 …………13分
…………13分
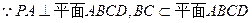
∴PA⊥BC
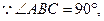
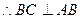
∴BC⊥平面PAB
又E是AB中点,
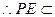 平面PAB
平面PAB∴BC⊥PE. …………6分
(II)建立直角坐标系
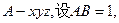
则B(1,0,0),C(1,1,0),P(0,0,1),
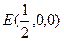
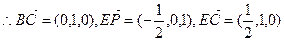
由(I)知,BC⊥平面PAE,
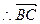 是平面PAE的法向量.
是平面PAE的法向量.设平面PEC的法向量为
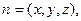
则
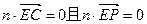
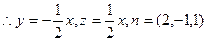
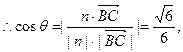
二面角C—PE—A的余弦值为
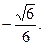 …………10分
…………10分(III)连结BC,设AB=a,
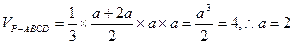
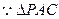 是直角三角形,
是直角三角形,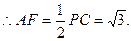 …………13分
…………13分
练习册系列答案
相关题目
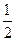 BD
BD
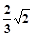
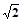
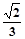
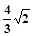
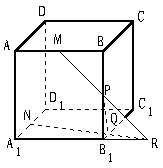
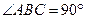 ,当E、F分别在线段AD、BC上,且
,当E、F分别在线段AD、BC上,且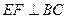 ,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
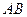 、
、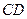 的长度分别等于
的长度分别等于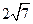 、
、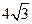 ,
,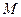 、
、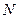 分别为
分别为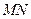 的最大值为5 ④
的最大值为5 ④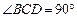 ,BC =" CD" = 1,AB⊥面BCD,
,BC =" CD" = 1,AB⊥面BCD,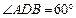 ,点E、F分别在AC、AD上,使面BEF⊥ACD,且EF∥CD,则平面BEF与平面BCD所成的二面角的正弦值为( )
,点E、F分别在AC、AD上,使面BEF⊥ACD,且EF∥CD,则平面BEF与平面BCD所成的二面角的正弦值为( )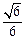
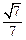
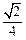
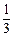
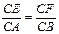 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).