题目内容
(本小题满分13分)如图甲,直角梯形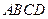 中,
中,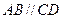 ,
,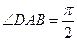 ,点
,点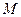 、
、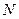 分别在
分别在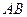 ,
,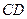 上,且
上,且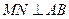 ,
,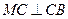 ,
,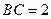 ,
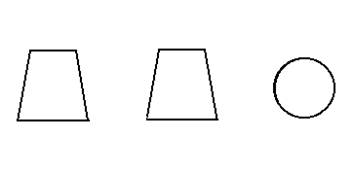
,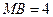 ,现将梯形
,现将梯形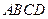 沿
沿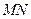 折起,使平面
折起,使平面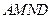 与平面
与平面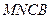 垂直(如图乙).
垂直(如图乙).
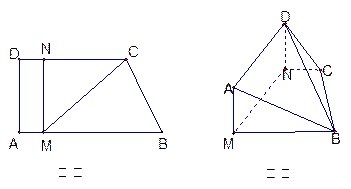
(Ⅰ)求证: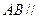 平面
平面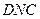 ;
;
(Ⅱ)当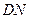 的长为何值时,
的长为何值时,
二面角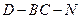 的大小为
的大小为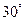 ?
?
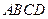 中,
中,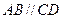 ,
,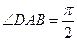 ,点
,点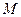 、
、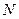 分别在
分别在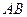 ,
,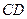 上,且
上,且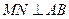 ,
,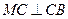 ,
,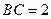 ,
,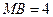 ,现将梯形
,现将梯形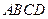 沿
沿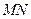 折起,使平面
折起,使平面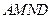 与平面
与平面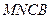 垂直(如图乙).
垂直(如图乙).
(Ⅰ)求证:
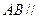 平面
平面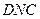 ;
;(Ⅱ)当
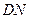 的长为何值时,
的长为何值时,二面角
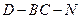 的大小为
的大小为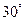 ?
?(Ⅰ)见解析 (Ⅱ) 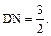
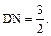
法一:(Ⅰ)MB//NC,MB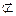 平面DNC,NC
平面DNC,NC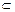 平面DNC,
平面DNC,
 MB//平面DNC.
MB//平面DNC.
同理MA//平面DNC,又MA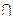 MB="M," 且MA,MB
MB="M," 且MA,MB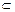 平面MAB.
平面MAB.
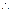
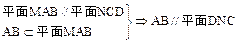 . (6分)
. (6分)
(Ⅱ)过N作NH 交BC延长线于H,连HN,
交BC延长线于H,连HN,
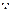 平面AMND
平面AMND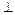 平面MNCB,DN
平面MNCB,DN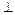 MN,
MN,
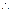 DN
DN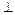 平面MBCN,从而
平面MBCN,从而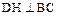 ,
,
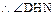 为二面角D-BC-N的平面角. (9分)
为二面角D-BC-N的平面角. (9分)
由MB=4,BC=2,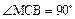 知
知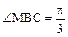 ,
,
 .
. 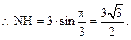 (10分)
(10分)
由条件知: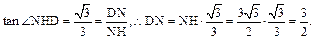 (13分)
(13分)
解法二:如图,以点N为坐标原点,以NM,NC,ND所在直线分别作为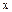 轴,
轴,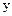 轴和
轴和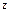 轴,建立空间直角坐标系
轴,建立空间直角坐标系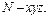 易得NC=3,MN=
易得NC=3,MN=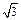 ,
,
设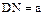 ,则
,则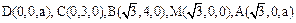 .
.
(I)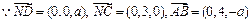 .
.
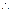
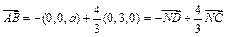 ,
,
∵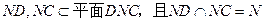 ,
,
∴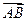 与平面
与平面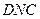 共面,又
共面,又 ,
,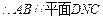 . (6分)
. (6分)
(II)设平面DBC的法向量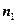
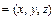 ,
,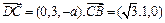
则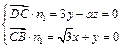 ,令
,令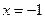 ,则
,则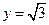 ,
,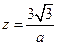
∴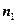
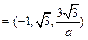 . (8分)又平面NBC的法向量
. (8分)又平面NBC的法向量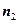
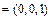 . (9分)
. (9分)
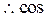
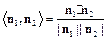
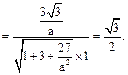
即: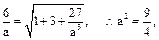 又
又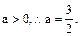 即
即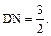 (13分)
(13分)
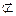 平面DNC,NC
平面DNC,NC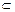 平面DNC,
平面DNC,
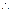 MB//平面DNC.
MB//平面DNC.同理MA//平面DNC,又MA
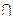 MB="M," 且MA,MB
MB="M," 且MA,MB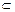 平面MAB.
平面MAB.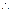
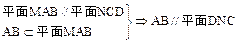 . (6分)
. (6分)(Ⅱ)过N作NH
 交BC延长线于H,连HN,
交BC延长线于H,连HN,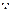 平面AMND
平面AMND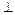 平面MNCB,DN
平面MNCB,DN MN,
MN,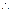 DN
DN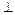 平面MBCN,从而
平面MBCN,从而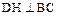 ,
,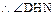 为二面角D-BC-N的平面角. (9分)
为二面角D-BC-N的平面角. (9分)由MB=4,BC=2,
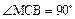 知
知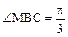 ,
, .
. 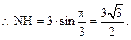 (10分)
(10分)由条件知:
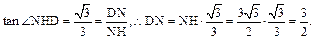 (13分)
(13分)解法二:如图,以点N为坐标原点,以NM,NC,ND所在直线分别作为
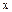 轴,
轴,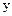 轴和
轴和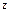 轴,建立空间直角坐标系
轴,建立空间直角坐标系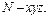 易得NC=3,MN=
易得NC=3,MN=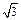 ,
,设
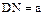 ,则
,则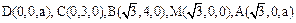 .
.(I)
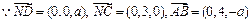 .
.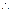
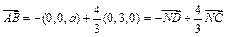 ,
,∵
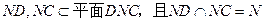 ,
,∴
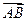 与平面
与平面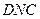 共面,又
共面,又 ,
,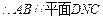 . (6分)
. (6分)(II)设平面DBC的法向量
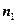
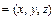 ,
,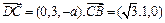
则
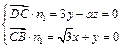 ,令
,令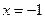 ,则
,则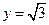 ,
,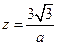
∴
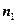
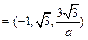 . (8分)又平面NBC的法向量
. (8分)又平面NBC的法向量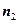
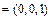 . (9分)
. (9分)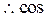
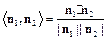
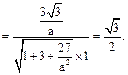
即:
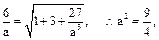 又
又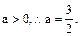 即
即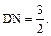 (13分)
(13分)
练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
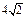 a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若
a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若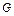 为
为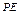 中点,求证:
中点,求证: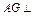 平面
平面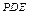 .
.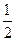 BD
BD

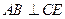
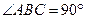 ,当E、F分别在线段AD、BC上,且
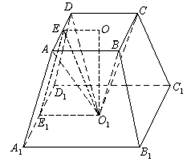
,当E、F分别在线段AD、BC上,且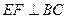 ,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
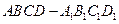 中,
中,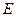 为
为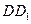 上的点、
上的点、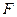 为
为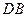 的中点.
的中点.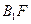 与平面
与平面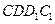 所成角的正弦值;
所成角的正弦值;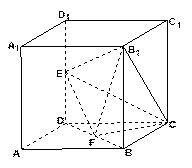 (Ⅱ)若直线
(Ⅱ)若直线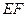 //平面
//平面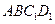 ,试确定点
,试确定点