题目内容
(本题满分14分)
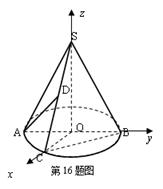
如图,圆锥的顶点是S,底面中心为O.OC是与底面直径AB垂直的一条半径,D是母线SC的中点.
(1)求证:BC与SA不可能垂直.
(2)设圆锥的高为4,异面直线AD与BC所成角的余弦值为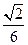 ,求圆锥的体积.
,求圆锥的体积.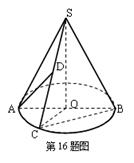
如图,圆锥的顶点是S,底面中心为O.OC是与底面直径AB垂直的一条半径,D是母线SC的中点.
(1)求证:BC与SA不可能垂直.
(2)设圆锥的高为4,异面直线AD与BC所成角的余弦值为
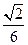 ,求圆锥的体积.
,求圆锥的体积.
(1)见解析
(2)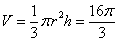
(2)
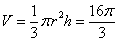
(1)
证法一:反证法:若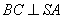 ,连AC,由AB是直径
,连AC,由AB是直径
则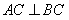 ,所以
,所以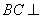 平面
平面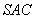 …………2分
…………2分
则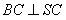 …………3分
…………3分
又圆锥的母线长相等,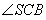 是等腰三角形SBC的底角,
是等腰三角形SBC的底角,
则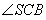 是锐角 …………4分
是锐角 …………4分
与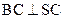 矛盾,所以BC与SA不垂直 …………6分
矛盾,所以BC与SA不垂直 …………6分
证法二:建立如图坐标系,设圆锥的高为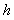 ,底面
,底面
 半径为
半径为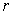 ,则
,则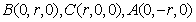
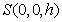 ,
,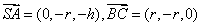 3分
3分
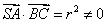 …………5分
…………5分
所以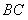 与SA不垂直 …………6分
与SA不垂直 …………6分
(2)建立如图坐标系,设底面半径为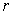 ,由高为4。则
,由高为4。则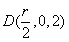 ,则
,则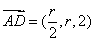 ,
,
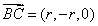 8分
8分

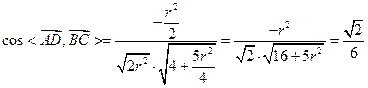 …………….10
…………….10
解得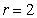 …….12分
…….12分
所以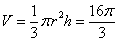 ………… 14分
………… 14分
证法一:反证法:若
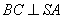 ,连AC,由AB是直径
,连AC,由AB是直径则
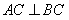 ,所以
,所以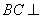 平面
平面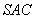 …………2分
…………2分则
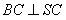 …………3分
…………3分又圆锥的母线长相等,
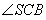 是等腰三角形SBC的底角,
是等腰三角形SBC的底角,则
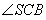 是锐角 …………4分
是锐角 …………4分与
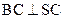 矛盾,所以BC与SA不垂直 …………6分
矛盾,所以BC与SA不垂直 …………6分证法二:建立如图坐标系,设圆锥的高为
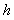 ,底面
,底面 半径为
半径为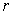 ,则
,则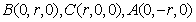
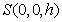 ,
,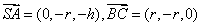 3分
3分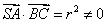 …………5分
…………5分所以
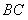 与SA不垂直 …………6分
与SA不垂直 …………6分(2)建立如图坐标系,设底面半径为
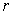 ,由高为4。则
,由高为4。则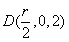 ,则
,则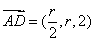 ,
,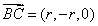 8分
8分
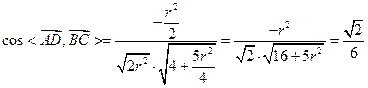 …………….10
…………….10解得
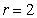 …….12分
…….12分所以
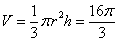 ………… 14分
………… 14分
练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
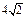 a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若
a,BC=DE=2a,∠EAB=∠ABC=∠DEA=90°.(1)若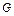 为
为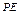 中点,求证:
中点,求证: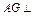 平面
平面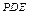 .
.
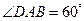
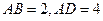
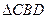
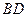
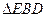
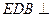
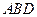
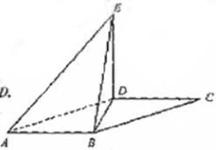
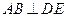 ; (Ⅱ)求三棱锥
; (Ⅱ)求三棱锥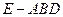 的侧面积。
的侧面积。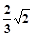
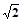
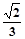
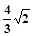
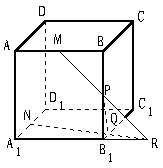
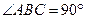 ,当E、F分别在线段AD、BC上,且
,当E、F分别在线段AD、BC上,且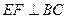 ,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
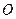 的半径是1,
的半径是1,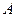 、
、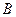 、
、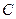 是球面上三点,已知
是球面上三点,已知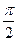 ,且二面角
,且二面角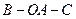 的大小是
的大小是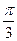 ,则从
,则从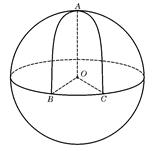
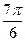
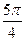
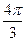
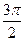
 BC中,PA⊥平面ABC、△ABC为正三角形,且PA=AB=2,则三棱锥P—ABC的侧视图面积为 。
BC中,PA⊥平面ABC、△ABC为正三角形,且PA=AB=2,则三棱锥P—ABC的侧视图面积为 。