题目内容
已知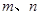 是两条不同的直线,
是两条不同的直线,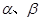 是两个不同的平面,有下列命题:
是两个不同的平面,有下列命题:
①若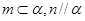 ,则
,则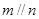 ; ②若
; ②若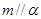 ,
,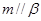 ,则
,则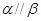 ;
;
③若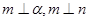 ,则
,则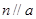 ; ④若
; ④若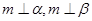 ,则
,则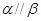 ;
;
其中真命题的个数是
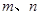 是两条不同的直线,
是两条不同的直线,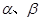 是两个不同的平面,有下列命题:
是两个不同的平面,有下列命题:①若
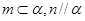 ,则
,则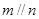 ; ②若
; ②若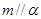 ,
,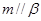 ,则
,则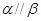 ;
;③若
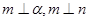 ,则
,则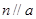 ; ④若
; ④若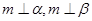 ,则
,则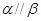 ;
;其中真命题的个数是
| A.0个 | B.1个 | C.2个 | D.3个 |
B
分析:在空间中:①由m?α,n∥α,知m,n可能平行,或异面;②由m∥α,m∥β,可得α,β平行,或相交;③由m⊥α,m⊥n,可得n∥α,或n?α;④由m⊥α,m⊥β,可得α∥β;综合可得答案.
解:①是假命题,因为当m?α,n∥α时,直线m,n不一定平行;
②是假命题,因为当m∥α,m∥β时,平面α,β可能平行,也可能相交;
③是假命题,因为当m⊥α,m⊥n时,不一定有n∥α,也可能是n?α;
④是真命题,因为当m⊥α,m⊥β时,由垂直与同一条直线的两个平面平行,得α∥β;
所以,真命题只有1个.
故答案为:B

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目

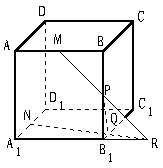
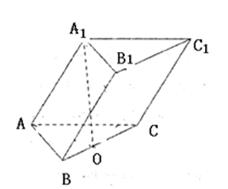
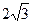 的正三角形,点A1在底面ABC上的射影O恰是BC的中点.
的正三角形,点A1在底面ABC上的射影O恰是BC的中点.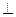 面BCC1B1;
面BCC1B1;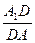 为何值时,BD⊥A1C1.
为何值时,BD⊥A1C1. ,当E、F分别在线段AD、BC上,且
,当E、F分别在线段AD、BC上,且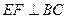 ,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
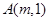 与
与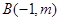 的直线与过点
的直线与过点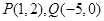 的直线垂直,则
的直线垂直,则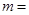 .
.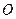 的半径是1,
的半径是1,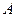 、
、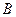 、
、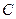 是球面上三点,已知
是球面上三点,已知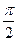 ,且二面角
,且二面角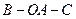 的大小是
的大小是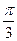 ,则从
,则从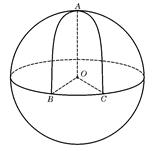
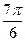
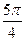
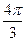
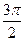
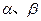 是两个不同的平面,给出下列四个命题:
是两个不同的平面,给出下列四个命题: 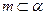 ,
,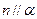 ,则
,则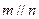 ; ②若
; ②若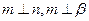 ,则
,则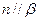 ;
;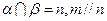 ,则
,则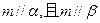 ; ④若
; ④若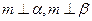 ,则
,则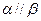 .
.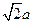 be the length of two sides of a rectangle (矩形),rotate(旋转)the rectangle about its
be the length of two sides of a rectangle (矩形),rotate(旋转)the rectangle about its