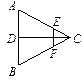题目内容
如图,四棱锥P—ABCD的底面是正方形,PA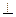 底面ABCD,PA=2,
底面ABCD,PA=2,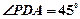 ,
,

点E,F分别为棱AB,PD的中点。
(I)在现有图形中,找出与AF平行的平面,并给出证明;
(II)判断平面PCE与平面PCD是否垂直?若垂直,给出证明;若不垂直,说明理由。
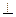 底面ABCD,PA=2,
底面ABCD,PA=2,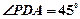 ,
,
点E,F分别为棱AB,PD的中点。
(I)在现有图形中,找出与AF平行的平面,并给出证明;
(II)判断平面PCE与平面PCD是否垂直?若垂直,给出证明;若不垂直,说明理由。
(1)见解析(2)垂直
(I)平面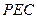 与
与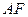 平行, 取
平行, 取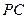 中点
中点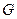 ,连
,连 ,因为
,因为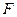 是
是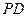 中点,
中点,

所以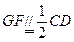 ,在正方形
,在正方形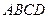 中,
中,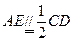 ,所以
,所以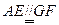 ,
,
所以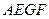 为平行四边形,
为平行四边形,
所以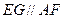 ,所以
,所以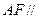 平面
平面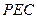
(II)由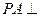 平面
平面 ,所以
,所以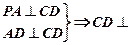 面
面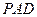 ,又
,又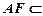 面
面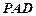 ,
,
所以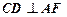 ,由(I)知
,由(I)知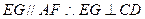 ,易证
,易证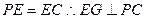
所以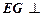 面
面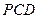 ,又
,又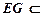 面
面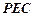 ,所以,面PCD
,所以,面PCD 面PEC…………12分
面PEC…………12分
(也可用空间向量法)
以A为原点AB 为X轴、AD为Y轴、 AP为Z轴,建立空间坐标系。…1分
易求A(0,0,0),F(0,1,1),G(1,1,1),E(1,0,0),
P(0,0,2),D(0,2,0),C(2,2,0)
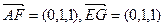 ,所以AF//面PEG。
,所以AF//面PEG。
设面PCD的法向量为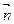 =(x,y,z),由
=(x,y,z),由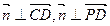 D得x=0,y=z.
D得x=0,y=z.
令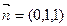 ,设面PEC的法向量为
,设面PEC的法向量为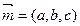 ,
,
由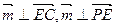 得
得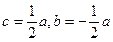 ,可令
,可令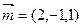
因为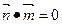 ,所以,面PCD
,所以,面PCD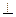 面PEC
面PEC
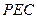 与
与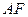 平行, 取
平行, 取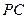 中点
中点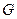 ,连
,连 ,因为
,因为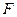 是
是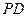 中点,
中点,
所以
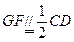 ,在正方形
,在正方形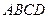 中,
中,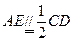 ,所以
,所以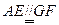 ,
,所以
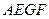 为平行四边形,
为平行四边形,所以
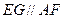 ,所以
,所以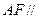 平面
平面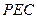
(II)由
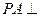 平面
平面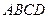 ,所以
,所以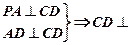 面
面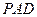 ,又
,又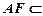 面
面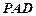 ,
,所以
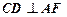 ,由(I)知
,由(I)知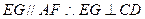 ,易证
,易证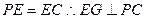
所以
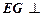 面
面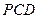 ,又
,又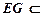 面
面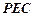 ,所以,面PCD
,所以,面PCD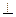 面PEC…………12分
面PEC…………12分(也可用空间向量法)
以A为原点AB 为X轴、AD为Y轴、 AP为Z轴,建立空间坐标系。…1分
易求A(0,0,0),F(0,1,1),G(1,1,1),E(1,0,0),
P(0,0,2),D(0,2,0),C(2,2,0)
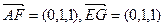 ,所以AF//面PEG。
,所以AF//面PEG。设面PCD的法向量为
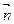 =(x,y,z),由
=(x,y,z),由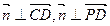 D得x=0,y=z.
D得x=0,y=z.令
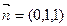 ,设面PEC的法向量为
,设面PEC的法向量为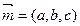 ,
,由
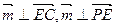 得
得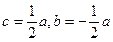 ,可令
,可令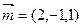
因为
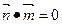 ,所以,面PCD
,所以,面PCD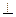 面PEC
面PEC
练习册系列答案
相关题目
 的底面为直角梯形,
的底面为直角梯形, ,
, ,
, ,
, ,
, 底面
底面 ,
, 为
为 的中点.
的中点. 平面
平面 ;
; 与平面
与平面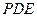 所成的角;
所成的角; 到平面
到平面
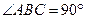 ,当E、F分别在线段AD、BC上,且
,当E、F分别在线段AD、BC上,且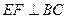 ,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
,AD=4,CB=6,AE=2,现将梯形ABCD沿EF折叠,使平面ABFE与平面EFCD垂直。
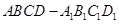 ,的棱长为1,
,的棱长为1,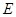 为
为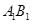 的中点,则下列五个命题:
的中点,则下列五个命题: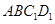 ,的距离为
,的距离为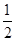
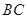 与平面
与平面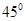
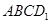 ,在正方体六个面内形成六个射影,其面积的最小值是
,在正方体六个面内形成六个射影,其面积的最小值是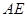 与
与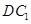 所成的角
所成的角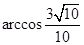
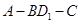 的大小为
的大小为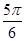
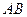 、
、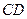 的长度分别等于
的长度分别等于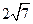 、
、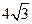 ,
,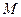 、
、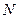 分别为
分别为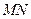 的最大值为5 ④
的最大值为5 ④
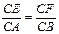 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).