题目内容
已知以T=4为周期的函数f(x)在(-1,3]上的解析式为f(x)=
,其中m>0,若方程3f(x)=x恰有5个实数解,则m的取值范围为______.
|
根据函数f(x)在(-1,3]上的解析式为f(x)=
,其中m>0,
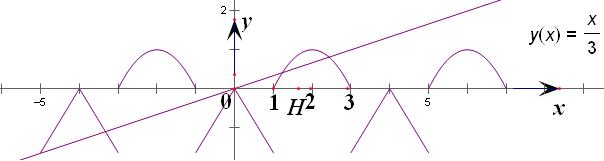
画出函数图象,再结合周期性画出函数图象
方程3f(x)=x恰有5个实数解即y=f(x)与y=
有五个交点
根据图象可知在[0,+∞)有三个交点
要使-m|x+4|=
在(-5,-3]上有两交点,-m|x+8|=
在(-9,-7]上没有交点
∴m∈(
,
]
故答案为:(
,
]
|
画出函数图象,再结合周期性画出函数图象
方程3f(x)=x恰有5个实数解即y=f(x)与y=
| x |
| 3 |
根据图象可知在[0,+∞)有三个交点
要使-m|x+4|=
| x |
| 3 |
| x |
| 3 |
∴m∈(
| 5 |
| 3 |
| 7 |
| 3 |
故答案为:(
| 5 |
| 3 |
| 7 |
| 3 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
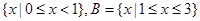 ,函数
,函数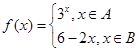 ,当
,当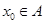 且
且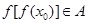 时,
时,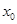 的取值范围是 。
的取值范围是 。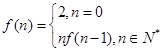 ,则
,则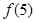 的值是( )
的值是( )