题目内容
设函数f(x)=x+a
(a∈R).
(1)若a=1,求f(x)的值域;
(2)若不等式f(x)≤2对x∈[-8,-3]恒成立,求实数a的取值范围.
| 1-x |
(1)若a=1,求f(x)的值域;
(2)若不等式f(x)≤2对x∈[-8,-3]恒成立,求实数a的取值范围.
(1)a=1时,f(x)=x+
,(x≤1),
令t=
,则t≥0,
则x=1-t2,
∴y=1-t2+t=-(t-
)2+
,
∵t≥0,
∴y≥
,
函数f(x)的值域是[
,+∞).
(2)令t=
,x∈[-8,-3],则x=1-t2,2≤t≤3,
则y=1-t2+at,
若不等式f(x)≤2对x∈[-8,-3]恒成立,
则等价为1-t2+at≤2对t∈[2,3]恒成立,
即a≤t+
对t∈[2,3]恒成立,
令g(t)=t+
,t∈[2,3],
则函数g(t)在[2,3]上是一个增函数,
∴g(t)的最小值为g(2)=
,
∴a≤
,
即a的取值范围为(-∞,
].
| 1-x |
令t=
| 1-x |
则x=1-t2,
∴y=1-t2+t=-(t-
| 1 |
| 2 |
| 5 |
| 4 |
∵t≥0,
∴y≥
| 5 |
| 4 |
函数f(x)的值域是[
| 5 |
| 4 |
(2)令t=
| 1-x |
则y=1-t2+at,
若不等式f(x)≤2对x∈[-8,-3]恒成立,
则等价为1-t2+at≤2对t∈[2,3]恒成立,
即a≤t+
| 1 |
| t |
令g(t)=t+
| 1 |
| t |
则函数g(t)在[2,3]上是一个增函数,
∴g(t)的最小值为g(2)=
| 5 |
| 2 |
∴a≤
| 5 |
| 2 |
即a的取值范围为(-∞,
| 5 |
| 2 |

练习册系列答案
相关题目
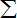
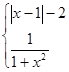
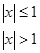 ,则f [ f (
,则f [ f (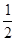 )]=
)]=