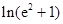题目内容
对于函数y=f（x），x∈D，如果存在非零常数T，使对任意的x∈D都有f（x+t）=f（x）成立，就称T为该函数的周期．请根据以上定义解答下列问题：若y=f（x）是R上的奇函数，且满足f（x+5）=f（x），当x∈（0，2）时，f（x）=2x2，则f（2014）=______．
由周期的定义可知若f（x+5）=f（x），则函数的周期T=5，
则f（2014）=f（402×5+4）=f（4）=f（4-5）=f（-1），
∵y=f（x）是R上的奇函数，当x∈（0，2）时，f（x）=2x2，
∴f（-1）=-f（1）=-2，
即f（2014）=f（-1）=-f（1）=-2．
故答案为：-2．
则f（2014）=f（402×5+4）=f（4）=f（4-5）=f（-1），
∵y=f（x）是R上的奇函数，当x∈（0，2）时，f（x）=2x2，
∴f（-1）=-f（1）=-2，
即f（2014）=f（-1）=-f（1）=-2．
故答案为：-2．
练习册系列答案
相关题目
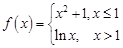，则
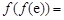（其中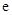
为自然对数的底数） （ ）
