题目内容
【题目】已知椭圆C方程:![]() +
+![]() =1(a>b>0),M(x0 , y0)是椭圆C上任意一点,F(c,0)是椭圆的右焦点.
=1(a>b>0),M(x0 , y0)是椭圆C上任意一点,F(c,0)是椭圆的右焦点.
(1)若椭圆的离心率为e,证明|MF|=a﹣ex0;
(2)已知不过焦点F的直线l与圆x2+y2=b2相切于点Q,并与椭圆C交于A,B两点,且A,B两点都在y轴的右侧,若a=2,求△ABF的周长.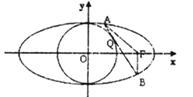
【答案】证明:(1)∵M(x0 , y0)是椭圆C上任意一点,椭圆的右准线方程为x=![]() ,
,
∴![]() =e
=e
∴|MF|=a﹣ex0;
(2)解:设A(x1 , y1),B(x2 , y2).(x1>0,x2>0),
连接OA,OQ,在△OAQ中,|AQ|2=x12+y12﹣b2 ,
∵y12=b2﹣![]() x12 ,
x12 ,
∴|AQ|2=1﹣![]() x12=e2x12;
x12=e2x12;
∴|AQ|=ex1 ,
同理:|BQ|=ex2 ,
∴|AB|=|AQ|+|BQ|=e(x1+x2)
∴|AB|+|AF|+|BF|=e(x1+x2)+a﹣ex1+a﹣ex2=2a
∴a=2时,△ABF的周长为4.
【解析】(1)利用椭圆的第二定义,即可得出结论;
(2)证明|AQ|=ex1 , |BQ|=ex2 , 即可求出△ABF的周长.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目


