题目内容
【题目】设函数![]() ,
,![]() .
.
(1)![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,函数
时,函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(3)若![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,且函数
轴平行,且函数![]() 在
在![]() 时,其图象上每一点处切线的倾斜角均为锐角,求
时,其图象上每一点处切线的倾斜角均为锐角,求![]() 的取值范围.
的取值范围.
【答案】(1) y=0.
(2)![]() .
.
(3)![]() .
.
【解析】分析:(1)先利用导数求切线的斜率,再写出切线的方程.(2)先求导得![]() ,转化为
,转化为![]() 与
与![]() 的图像的交点有两个,再利用数形结合分析两个函数的图像得到
的图像的交点有两个,再利用数形结合分析两个函数的图像得到![]() 的取值范围.(3)先转化为当
的取值范围.(3)先转化为当![]() 时,
时,![]() 恒成立,即
恒成立,即
![]() ,再构造函数
,再构造函数![]() 求其最小值,令其最小值大于零,得a的取值范围.
求其最小值,令其最小值大于零,得a的取值范围.
详解:(1)由题得![]() 所以切线方程为y=0.
所以切线方程为y=0.
(2) 当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 有两个极值点就是方程
有两个极值点就是方程![]() 有两个解,
有两个解,
即![]() 与
与![]() 的图像的交点有两个.
的图像的交点有两个.
∵![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.![]() 有极大值
有极大值![]() 又因为
又因为![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
当![]() 时
时![]() 与
与![]() 的图像的交点有0个;
的图像的交点有0个;
当![]() 或
或![]() 时
时![]() 与
与![]() 的图像的交点有1个;
的图像的交点有1个;
当![]() 时
时![]() 与
与![]() 的图象的交点有2个;
的图象的交点有2个;
综上![]() .
.
(3)函数![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,
轴平行,
所以![]() 且
且![]() ,因为
,因为![]() ,
,
所以![]() 且
且![]() ;
;
![]() 在
在![]() 时,其图像的每一点处的切线的倾斜角均为锐角,
时,其图像的每一点处的切线的倾斜角均为锐角,
即当![]() 时,
时,![]() 恒成立,即
恒成立,即
![]() ,
,
令![]() ,∴
,∴![]()
设![]() ,
,![]() ,因为
,因为![]() ,所以
,所以![]() ,∴
,∴![]() ,
,
∴![]() 在
在![]() 单调递增,即
单调递增,即![]() 在
在![]() 单调递增,
单调递增,
∴![]() ,当
,当![]() 且
且![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递增;
单调递增;
∴![]() 成立
成立
当![]() ,因为
,因为![]() 在
在![]() 单调递增,所以
单调递增,所以![]() ,
,![]() ,
,
所以存在![]() 有
有![]() ;
;
当![]() 时,
时,![]() ,
,![]() 单调递减,所以有
单调递减,所以有![]() ,
,![]() 不恒成立;
不恒成立;
所以实数![]() 的取值范围为
的取值范围为![]() .
.

【题目】某汽车公司对最近6个月内的市场占有率进行了统计,结果如表;
月份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
市场占有率 | 11 | 13 | 16 | 15 | 20 | 21 |
(1)可用线性回归模型拟合![]() 与
与![]() 之间的关系吗?如果能,请求出
之间的关系吗?如果能,请求出![]() 关于
关于![]() 的线性回归方程,如果不能,请说明理由;
的线性回归方程,如果不能,请说明理由;
(2)公司决定再采购![]() 两款车扩大市场,
两款车扩大市场, ![]() 两款车各100辆的资料如表:
两款车各100辆的资料如表:
车型 | 报废年限(年) | 合计 | 成本 | |||
1 | 2 | 3 | 4 | |||
| 10 | 30 | 40 | 20 | 100 | 1000元/辆 |
| 15 | 40 | 35 | 10 | 100 | 800元/辆 |
平均每辆车每年可为公司带来收入![]() 元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
元,不考虑采购成本之外的其他成本,假设每辆车的使用寿命部是整数年,用每辆车使用寿命的频率作为概率,以每辆车产生利润的平均数作为决策依据,应选择采购哪款车型?
参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数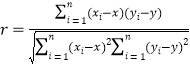 ;
;
回归直线方程为![]() ,其中
,其中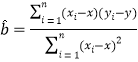 ,
,![]() .
.