Question

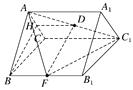
【题目】如图，正三棱柱ABC－A1B1C1的各棱长都等于2，D在AC1上，F为BB1的中点，且FD⊥AC1，有下述结论：

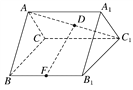
①AC1⊥BC；

②＝1；

③平面FAC1⊥平面ACC1A1；

④三棱锥D－ACF的体积为.

其中正确结论的个数为(　　)

A. 1 B. 2

C. 3 D. 4

Answer 1

【答案】C

【解析】BC⊥CC1，但BC不垂直于AC，故BC不垂直于平面ACC1A1，所以AC1与BC不垂直，故①错误；

连接AF，C1F，可得AF＝C1F＝.

因为FD⊥AC1，所以可得D为线段AC1的中点，故②正确；

取AC的中点为H，连接BH，DH，

因为该三棱柱是正三棱柱，所以CC1⊥底面ABC，

因为BH底面ABC，所以CC1⊥BH，

因为底面ABC为正三角形，可得BH⊥AC，

又AC∩CC1＝C，所以BH⊥侧面ACC1A1.

因为D和H分别为AC1，AC的中点，所以DH∥CC1∥BF，

DH＝BF＝CC1，可得四边形BFDH为平行四边形，所以FD∥BH，

所以可得FD⊥平面ACC1A1，因为FD平面FAC1，

所以平面FAC1⊥平面ACC1A1，故③正确；

VD－ACF＝VF－ADC＝·FD·S△ACD＝，故④正确．

即正确结论的个数为3个.

本题选择C选项.