Question

【题目】已知函数f(x)＝ex－e－x(x∈R，且e为自然对数的底数).

(1)判断函数f(x)的单调性与奇偶性；

(2)是否存在实数t，使不等式f(x－t)＋f(x2－t2)≥0对一切x∈R都成立？若存在，求出t；若不存在，请说明理由.

Answer 1

【答案】(1)见解析.(2)t＝－.

【解析】(1)∵f(x)＝ex－x，且y＝ex是增函数，

y＝－x是增函数，∴f(x)是增函数．

由于f(x)的定义域为R，且f(－x)＝e－x－ex＝－f(x)，

∴f(x)是奇函数．

(2)由(1)知f(x)是增函数和奇函数，

∴f(x－t)＋f(x2－t2)≥0对一切x∈R恒成立

f(x2－t2)≥f(t－x)对一切x∈R恒成立

x2－t2≥t－x对一切x∈R恒成立

t2＋t≤x2＋x对一切x∈R恒成立

2≤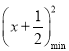对一切x∈R恒成立

2≤0t＝－.

即存在实数t＝－，使不等式f(x－t)＋f(x2－t2)≥0对一切x都成立．