题目内容
4.若关于x的不等式ax2-6x+a2<0(a∈R)的解集为(-∞,m)∪(1,+∞),则m=-3.分析 利用一元二次不等式的解集和对应方程之间的关系,将不等式转化为为一元二次方程根的问题进行求解即可.
解答 解:∵ax2-6x+a2<0(a∈R)的解集为(-∞,m)∪(1,+∞),
∴1和m是对应方程ax2-6x+a2=0的两个根,且a<0,m<1,
根据根与系数之间的关系得m=a,1+m=$\frac{6}{a}$,
即1+m=$\frac{6}{m}$,
解得m=-3或m=2(舍去),
∴m=-3.
故答案为:-3.
点评 本题主要考查一元二次不等式的应用,将不等式转化为为一元二次方程根是解决本题的关键.

练习册系列答案
相关题目
12.将编号分别为1,2,3,4,5的五份奖品分给四个人,每人至少1份,且分给同一个人的2份奖品需连号,则不同的分法种数是( )
| A. | 24 | B. | 96 | C. | 192 | D. | 240 |
19.从3名男生和2名女生中任选2名学生参加演讲比赛,在选出的这2人中,设事件A={恰有1名男生},事件B={至少有1名男生},事件C={全是女生},则下列结论正确的是( )
| A. | A与B互斥 | B. | A与B对立 | C. | A与C对立 | D. | B与C对立 |
9.从1,2,3,4中任取不同的数字构成一个两位数,则这个数小于20的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
16.某市有大型超市100家,中型超市200家,小型超市700家,为了了解各类超市的营业情况,现按分层抽样抽取一个容量为100的样本,应抽取中型超市( )
| A. | 70家 | B. | 50家 | C. | 20家 | D. | 10家 |
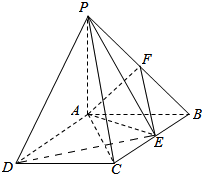 如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E边BC上移动.
如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E边BC上移动.