题目内容
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,原点为
,原点为![]() ,椭圆
,椭圆![]() 的动弦
的动弦![]() 过焦点
过焦点![]() 且不垂直于坐标轴,弦
且不垂直于坐标轴,弦![]() 的中点为
的中点为![]() ,过
,过![]() 且垂直于线段
且垂直于线段![]() 的直线交射线
的直线交射线![]() 于点
于点![]() .
.
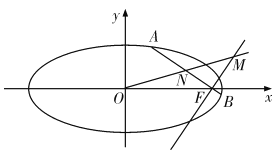
(Ⅰ)证明:点![]() 在定直线上;
在定直线上;
(Ⅱ)当![]() 最大时,求
最大时,求![]() 的面积.
的面积.
【答案】(Ⅰ)见解析.( Ⅱ) ![]() .
.
【解析】
(I)求出椭圆![]() 的右焦点F的坐标,设AB所在直线为:
的右焦点F的坐标,设AB所在直线为:![]() (k≠0),且A(x1,y1),B(x2,y2).联立直线与椭圆的方程组,通过韦达定理,求出中点坐标,求出ON的方程,与FM所在的直线方程联立,解得点M坐标即可求出M在定直线
(k≠0),且A(x1,y1),B(x2,y2).联立直线与椭圆的方程组,通过韦达定理,求出中点坐标,求出ON的方程,与FM所在的直线方程联立,解得点M坐标即可求出M在定直线![]() 上;(Ⅱ)由(I)可设点M的坐标为
上;(Ⅱ)由(I)可设点M的坐标为![]() ,且F(1,0),求出
,且F(1,0),求出![]() 向量坐标,利用向量的数量积求出cos∠OMF取得最小值时,∠OMF最大,由此可得M的坐标及直线AB的方程,利用弦长公式和点到线的距离公式求解三角形的面积的即可.
向量坐标,利用向量的数量积求出cos∠OMF取得最小值时,∠OMF最大,由此可得M的坐标及直线AB的方程,利用弦长公式和点到线的距离公式求解三角形的面积的即可.
(I)椭圆![]() 的右焦点
的右焦点![]() 的坐标为
的坐标为![]() ,
,
设![]() 所在直线为
所在直线为![]()
![]() ,且
,且![]()
![]() ,
,
联立 ,得
,得![]() ,
,
其中![]() ,
,![]() ,点
,点![]() 坐标为
坐标为![]() ,
,
联立 得点
得点![]() 坐标为
坐标为![]() ,
,
所以点![]() 坐标满足直线方程
坐标满足直线方程![]() ,故点
,故点![]() 在定直线上.
在定直线上.
(Ⅱ)由(I)可设![]() 坐标为
坐标为![]() ,
,![]() ,不妨取
,不妨取![]() ,
,
则![]() ,
,![]() ,
,

![]()
 ,当且仅当
,当且仅当![]() 时等号成立,
时等号成立,
因为![]() 在
在![]() 上为减函数,所以
上为减函数,所以![]() 时,
时,![]() 取到最大值.
取到最大值.
由![]() ,得
,得![]() 坐标为
坐标为![]() ,
,![]() ,
,
直线![]() 方程
方程![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,![]()
![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以![]() 的面积
的面积![]()

【题目】苹果是人们日常生活中常见的营养型水果.某地水果批发市场销售来自5个不同产地的富士苹果,各产地的包装规格相同,它们的批发价格(元/箱)和市场份额如下:
产地 |
|
|
|
|
|
批发价格 |
|
|
|
|
|
市场份额 |
|
|
|
|
|
市场份额亦称“市场占有率”.指某一产品的销售量在市场同类产品中所占比重.
(1)从该地批发市场销售的富士苹果中随机抽取一箱,求该箱苹果价格低于![]() 元的概率;
元的概率;
(2)按市场份额进行分层抽样,随机抽取![]() 箱富士苹果进行检验,
箱富士苹果进行检验,
①从产地![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;
的值;
②从这![]() 箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
(3)由于受种植规模和苹果品质的影响,预计明年产地![]() 的市场份额将增加
的市场份额将增加![]() ,产地
,产地![]() 的市场份额将减少
的市场份额将减少![]() ,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱
,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱![]() 元,明年苹果的平均批发价为每箱
元,明年苹果的平均批发价为每箱![]() 元,比较
元,比较![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
【题目】据《人民网》报道,“美国国家航空航天局( NASA)发文称,相比20年前世界变得更绿色了.卫星资料显示中国和印度的行动主导了地球变绿.”据统计,中国新增绿化面积的42%来自于植树造林,下表是中国十个地区在2017年植树造林的相关数据.(造林总面积为人工造林、飞播造林、新封山育林、退化林修复、人工更新的面积之和)
单位:公顷
造林方式 | ||||||
地区 | 造林总面积 | 人工造林 | 飞播造林 | 新封山育林 | 退化林修复 | 人工更新 |
内蒙 | 618484 | 311052 | 74094 | 136006 | 90382 | 6950 |
河北 | 583361 | 345625 | 33333 | 135107 | 65653 | 3643 |
河南 | 149002 | 97647 | 13429 | 22417 | 15376 | 133 |
重庆 | 226333 | 100600 | 62400 | 63333 | ||
陕西 | 297642 | 33602 | 63865 | 16067 | ||
甘肃 | 325580 | 260144 | 57438 | 7998 | ||
新疆 | 263903 | 118105 | 6264 | 126647 | 10796 | 2091 |
青海 | 178414 | 16051 | 159734 | 2629 | ||
宁夏 | 91531 | 58960 | 22938 | 8298 | 1335 | |
北京 | 19064 | 10012 | 4000 | 3999 | 1053 | |
(I)请根据上述数据分别写出在这十个地区中人工造林面积与造林总面积的比值最大和最小的地区;
(Ⅱ)在这十个地区中,任选一个地区,求该地区人工造林面积占造林总面积的比值超过![]() 的概率是多少?
的概率是多少?
(Ⅲ)在这十个地区中,从新封山育林面积超过五万公顷的地区中,任选两个地区,记X为这两个地区中退化林修复面积超过六万公顷的地区的个数,求X的分布列及数学期望.
【题目】微信已成为人们常用的社交软件,“微信运动”是由腾讯开发的一个类似计步数据库的公众账号.手机用户可以通过关注“微信运动”公众号查看自己每天行走的步数,同时也可以和好友进行运动量的PK或点赞.现从小明的微信朋友圈内随机选取了50人(男、女各25人),并记录了他们某一天的走路步数,并将数据整理如下表:
步数 性别 | 0~3000 | 3001~6000 | 6001~9000 | 9001~12000 | >12000 |
男 | 1 | 1 | 3 | 15 | 5 |
女 | 0 | 4 | 11 | 8 | 2 |
若某人一天走路的步数超过9000步被系统评定为“积极型”,否则被系统评定为“懈怠型”。
(1)利用样本估计总体的思想,估计小明的所有微信好友中每日走路步数超过12000步的概率;
(2)根据题意完成下面的2×2列联表,并据此判断能否有99.5%的把握认为“评定类型”与“性别”有关?
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
附: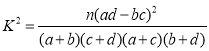 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |