题目内容
【题目】如图在直角梯形ABCD中,AB//CD,AB⊥BC,AB=3BE=3![]() ,CD=2
,CD=2![]() ,AD=2.将△ADE沿DE折起,使平面ADE⊥平面BCDE.
,AD=2.将△ADE沿DE折起,使平面ADE⊥平面BCDE.
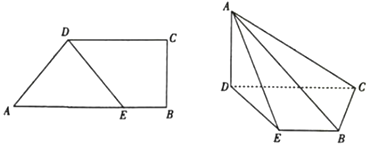
(1)证明:BC⊥平面ACD;
(2)求直线AE与平面ABC所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)在直角梯形ABCD中,由平面几何知识可证![]() ,从而由面面垂直性质定理得线面垂直,可得线线垂直
,从而由面面垂直性质定理得线面垂直,可得线线垂直![]() ,于是可证线面垂直;
,于是可证线面垂直;
(2)以D为原点,过D作CB的平行线为x轴,DC为y轴,DA为z轴,建立空间直角坐标系,由向量法示得线面角的正弦值.
(1)证明:在直角梯形ABCD中,AB//CD,AB⊥BC,
AB=3BE=3![]() ,CD=2
,CD=2![]() ,AD=2.
,AD=2.
∴![]() ,
,![]() ,
,![]()
在直角梯形![]() 中可得
中可得![]() ,
,
∴AD2+DE2=AE2,∴AD⊥DE,
∵平面ADE⊥平面BCDE,平面ADE∩平面BCDE=DE.
∴AD⊥平面BCDE,∵CB平面BCDE,∴AD⊥BC,
∵AB⊥BC,∴CD⊥BC,
又CD∩AD=D,∴BC⊥平面ACD.

(2)解:以D为原点,过D作CB的平行线为x轴,DC为y轴,DA为z轴,建立空间直角坐标系,
A(0,0,2),E(![]() ,
,![]() ,0),B(
,0),B(![]() ,2
,2![]() ,0),C(0,2
,0),C(0,2![]() ,0),
,0),
![]() (
(![]() ,﹣2),
,﹣2),![]() (0,﹣2
(0,﹣2![]() ,2),
,2),![]() (
(![]() ,0,0),
,0,0),
设平面ABC的法向量![]() (x,y,z),
(x,y,z),
则 ,取y=1,则
,取y=1,则![]() (0,1,
(0,1,![]() ),
),
设直线AE与平面ABC所成角为θ,
则直线AE与平面ABC所成角的正弦值为sinθ .
.

 阅读快车系列答案
阅读快车系列答案【题目】某中学为研究学生的身体素质与体育锻炼时间的关系,对该校300名高三学生平均每天体育锻炼时间进行调查,如表:(平均每天锻炼的时间单位:分钟).
平均每天锻炼的时间/分钟 |
|
|
|
|
|
|
总人数 | 34 | 51 | 59 | 66 | 65 | 25 |
将学生日均体育锻炼时间在![]() 的学生评价为“锻炼达标”.
的学生评价为“锻炼达标”.
(1)请根据上述表格中的统计数据填写下面的![]() 列联表;
列联表;
锻炼不达标 | 锻炼达标 | 合计 | |
男 | |||
女 | 40 | 160 | |
合计 |
(2)通过计算判断,是否能在犯错误的概率不超过0.05的前提下认为“锻炼达标”与性别有关?
参考公式:![]() ,其中
,其中![]() .
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |