题目内容
11．由直线y=x-4，曲线y=$\sqrt{2x}$以及y=0所围成的图形的面积为（ ）| A． | $\frac{40}{3}$ | B． | $\frac{34}{3}$ | C． | $\frac{64}{3}$ | D． | 16 |
分析 由题意画出图形，数形结合把曲边梯形的面积用定积分表示，求定积分得答案
解答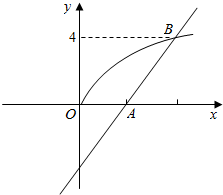 
解：如图，联立方程组得$\left\{\begin{array}{l}{y=x-4}\\{y=\sqrt{2x}}\end{array}\right.$，解得x=8，y=4，
由直线y=x-4，曲线y=$\sqrt{2x}$以及y=0所围成的图形的面积为：
S=${∫}_{0}^{4}$（y+4-$\frac{1}{2}$y2）dy=（$\frac{1}{2}$y2+4y-$\frac{1}{6}$y3）|${\;}_{0}^{4}$=8+16-$\frac{32}{3}$=$\frac{40}{3}$，
故选：A．
点评 本题考查了定积分，考查了定积分的几何意义，是中档题
练习册系列答案
相关题目
3．设a=（$\frac{3}{4}$）${\;}^{\frac{2}{3}}$，b=（$\frac{2}{3}$）${\;}^{\frac{3}{4}}$，c=log${\;}_{\frac{2}{3}}$$\frac{4}{3}$，则a，b，c的大小关系是（ ）
| A． | a＞c＞b | B． | a＞b＞c | C． | c＞b＞a | D． | b＞c＞a |