题目内容
【题目】如图,△ABC中,∠BAC=90°,∠ABC=30°.△ABD中,∠ADB=90°,∠ABD=45°,且AC=1.将△ABD沿边AB折叠后,

(1)若二面角C—AB—D为直二面角,则直线CD与平面ABC所成角的正切值为_______;
(2)若二面角C—AB—D的大小为150°,则线段CD的长为_______.
【答案】![]()
![]()
【解析】
作出二面角![]() 的平面角.
的平面角.
(1)当二面角![]() 为直角时,判断出直线
为直角时,判断出直线![]() 与平面
与平面![]() 所成的角,解直角三角形求得线面角的正切值.
所成的角,解直角三角形求得线面角的正切值.
(2)当二面角![]() 大小为
大小为![]() 时,结合余弦定理进行解三角形,由此求得
时,结合余弦定理进行解三角形,由此求得![]() 的长.
的长.
依题意![]() ABC中,∠BAC=90°,∠ABC=30°.△ABD中,∠ADB=90°,∠ABD=45°,且AC=1.所以
ABC中,∠BAC=90°,∠ABC=30°.△ABD中,∠ADB=90°,∠ABD=45°,且AC=1.所以![]() ,
,![]() .设
.设![]() 分别是
分别是![]() 的中点,所以
的中点,所以![]() ,
,![]()
![]() ,所以
,所以![]() 是二面角
是二面角![]() 的平面角,
的平面角,![]() .
.
(1)当二面角![]() 为直角时,由于
为直角时,由于![]() ,根据面面垂直的性质定理可知
,根据面面垂直的性质定理可知![]() 平面
平面![]() ,所以
,所以![]() 是直线img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/17/39a1a048/SYS202011261741258328971401_DA/SYS202011261741258328971401_DA.004.png" width="29" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />与平面
是直线img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/17/39a1a048/SYS202011261741258328971401_DA/SYS202011261741258328971401_DA.004.png" width="29" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />与平面![]() 所成的角.在
所成的角.在![]() 中
中 .
.
(2)当二面角![]() 大小为
大小为![]() 时,即
时,即![]() ,在三角形
,在三角形![]() 中,由余弦定理得
中,由余弦定理得![]()
![]() .在三角形
.在三角形![]() 和三角形
和三角形![]() 中,
中,![]() ,由余弦定理得
,由余弦定理得![]() ,
,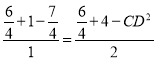 ,
,![]() .
.
故答案为:(1). ![]() (2).
(2). ![]()


练习册系列答案
相关题目