题目内容
2.在平面上有一个四边形ABCD,E,F,G,H分别是AB,BC,CD,DA的中点,求证:$\overrightarrow{EF}$=$\overrightarrow{HG}$.分析 根据条件画出图形,并连接AC,由中位线的性质即可得到EF∥HG,并且|EF|=|HG|,并由图形看出向量$\overrightarrow{EF}$,$\overrightarrow{HG}$同向,这样即可得到$\overrightarrow{EF}=\overrightarrow{HG}$.
解答 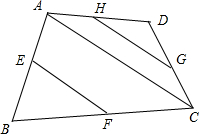 证明:如图,
证明:如图,
连接AC,E,F分别是AB,BC的中点;
即EF为△ABC的中位线;
∴EF∥AC,且$|EF|=\frac{|AC|}{2}$;
同理,HG∥AC,且$|HG|=\frac{|AC|}{2}$;
∴EF∥HG,且|EF|=|HG|,且向量$\overrightarrow{EF}$,$\overrightarrow{HG}$方向相同;
∴$\overrightarrow{EF}=\overrightarrow{HG}$.
点评 考查三角形中位线的性质,平行线的传递性,相等向量的概念.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
12.已知点A(1,$\sqrt{3}$),B(-1,-$\sqrt{3}$),则直线AB的倾斜角是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
10.下列关于斜二测画法下的直观图的说法正确的是( )
| A. | 互相垂直的两条直线的直观图一定是互相垂直的两条直线 | |
| B. | 梯形的直观图可能是平行四边形 | |
| C. | 矩形的直观图可能是梯形 | |
| D. | 正方形的直观图可能是平行四边形. |
7.已知A={x||x-1|>0},B={x|(x-1)2-3≥0},则A∩B=( )
| A. | (-∞,0)∪(2,+∞) | B. | (-∞,1-$\sqrt{3}$]∪[1+$\sqrt{3}$,+∞) | C. | (-∞,1-$\sqrt{3}$]∪[2,+∞) | D. | (-∞,0)∪[1+$\sqrt{3}$,+∞) |
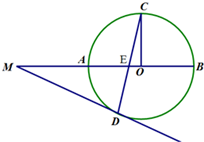 如图,圆O的半径OC垂直于直径AB,弦CD交半径OA于E,过D的切线与BA的延长线交于M.
如图,圆O的半径OC垂直于直径AB,弦CD交半径OA于E,过D的切线与BA的延长线交于M.