题目内容
12．已知点A（1，$\sqrt{3}$），B（-1，-$\sqrt{3}$），则直线AB的倾斜角是（ ）| A． | $\frac{π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |
分析 利用两点的坐标求出直线的斜率，再求出直线的倾斜角．
解答 解：∵点A（1，$\sqrt{3}$），B（-1，-$\sqrt{3}$），
∴直线AB的斜率是k=$\frac{-\sqrt{3}-\sqrt{3}}{-1-1}$=$\sqrt{3}$，
∴tanα=$\sqrt{3}$，且α∈[0，π），
∴倾斜角是α=$\frac{π}{3}$．
故选：A．
点评 本题考查了利用两点的坐标求直线的斜率与倾斜角的应用问题，是基础题目．
练习册系列答案
步步高达标卷系列答案
相关题目
2．
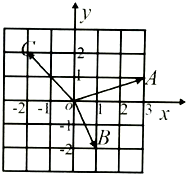如图，在复平面内，已知复数z1、z2、z3，对应的向量分别是$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$，（i是虚数单位），已知z=$\frac{{z}_{1}•{z}_{2}}{{z}_{3}}$则|$\overrightarrow{z}$+$\frac{\sqrt{11}}{2}$i|=（ ）
如图，在复平面内，已知复数z1、z2、z3，对应的向量分别是$\overrightarrow{OA}$，$\overrightarrow{OB}$，$\overrightarrow{OC}$，（i是虚数单位），已知z=$\frac{{z}_{1}•{z}_{2}}{{z}_{3}}$则|$\overrightarrow{z}$+$\frac{\sqrt{11}}{2}$i|=（ ）| A． | 3 | B． | $\sqrt{10+\sqrt{11}}$ | C． | $\sqrt{6+\sqrt{11}}$ | D． | $\frac{3}{2}$ |
3．若不等式组$\left\{\begin{array}{l}{|x|+|y|≤3}\\{y+3≤k（x+1）}\end{array}\right.$表示的平面区域是三角形，则实数k的取值范围是（ ）
| A． | -$\frac{3}{2}$＜k≤$\frac{3}{4}$ | B． | k＜-$\frac{3}{2}$或k≥$\frac{3}{4}$ | C． | -$\frac{3}{2}$＜k＜0或k≥$\frac{3}{4}$ | D． | k＜-$\frac{3}{2}$或0＜k≤$\frac{3}{4}$ |
7．
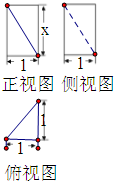如图是某几何体的三视图，则该几何体的体积等于$\frac{2}{3}$，则图中的x的值（ ）
如图是某几何体的三视图，则该几何体的体积等于$\frac{2}{3}$，则图中的x的值（ ）| A． | 2 | B． | 3 | C． | 1 | D． | $\frac{4}{3}$ |
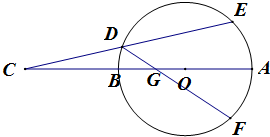如图，在⊙O直径AB的延长线上任取一点C，过点C做直线CE与⊙O交于点D、E，在⊙O上取一点F，使$\widehat{AE}=\widehat{AF}$，连接DF，交AB于G．