题目内容
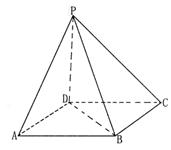
(12分)如图所示,已知ABCD是正方形,PD⊥平面ABCD,
PD=AD=2.
(1)求异面直线PC与BD所成的角;
(2)在线段PB上是否存在一点E,使PC⊥平面ADE?
若存在,确定E点的位置;若不存在,说明理由.
PD=AD=2.
(1)求异面直线PC与BD所成的角;
(2)在线段PB上是否存在一点E,使PC⊥平面ADE?
若存在,确定E点的位置;若不存在,说明理由.

如图建立空间直角坐标系,则D(0,0,0),
A(2,0,0),C(0,2,0),P(0,0,2),B(2,2,0),
(1)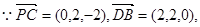
∴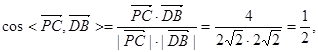
∴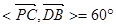 ,∴异面直线PC与BD所成的角为60°
,∴异面直线PC与BD所成的角为60°
(2)假设在PB上存在E点,使PC⊥平 ADE,记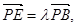

∴ 若PC⊥平面ADE,则有PC⊥AE,
若PC⊥平面ADE,则有PC⊥AE,
即 ,∴
,∴ 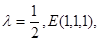
∴存在E点且E为PB的中点时,PC⊥平面ADE.
A(2,0,0),C(0,2,0),P(0,0,2),B(2,2,0),
(1)
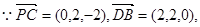
∴
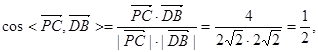
∴
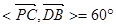 ,∴异面直线PC与BD所成的角为60°
,∴异面直线PC与BD所成的角为60°(2)假设在PB上存在E点,使PC⊥平 ADE,记
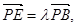

∴
 若PC⊥平面ADE,则有PC⊥AE,
若PC⊥平面ADE,则有PC⊥AE,即
 ,∴
,∴ 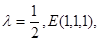
∴存在E点且E为PB的中点时,PC⊥平面ADE.
略

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
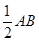 ,∠ACF=∠ADC=
,∠ACF=∠ADC=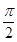 。
。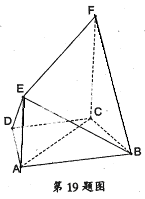
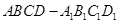 中,底面
中,底面 是边长为
是边长为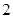 的正方形,
的正方形,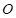 为
为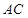 与
与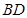 的交点,
的交点,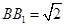 ,
,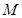 是线段
是线段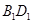 的中点.请建立空间直角坐标系解决以下问题:
的中点.请建立空间直角坐标系解决以下问题: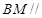 平面
平面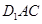 ;
;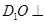 平面
平面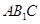 ;
;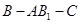 的大小.
的大小.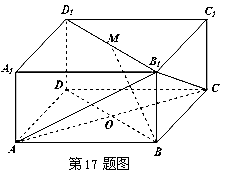
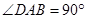 ,
,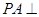 平面ABCD,PA=AB=BC=3,梯形上底AD=1。
平面ABCD,PA=AB=BC=3,梯形上底AD=1。 平面PAB;
平面PAB;
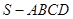 中,
中,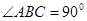 ,
,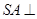 面
面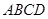 ,
, ,
,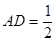 。
。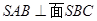 ;
; 的距离。
的距离。
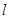 上有无数点不在平面
上有无数点不在平面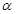 内,则
内,则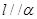
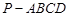 中,底面
中,底面 是直角梯形,
是直角梯形,
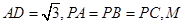 是线段
是线段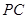 上不同于
上不同于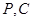 的任意一点,且
的任意一点,且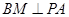

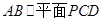 ;
;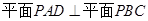 ;
;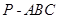 的体积。
的体积。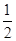 AB=a,E是AB的中点,将ΔADE沿DE折起,使点A折到点P的位置,且二面角P-DE-C的大小为120°.
AB=a,E是AB的中点,将ΔADE沿DE折起,使点A折到点P的位置,且二面角P-DE-C的大小为120°.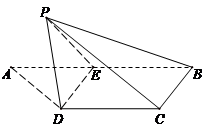
 形
形