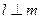题目内容
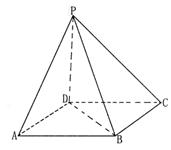
(本小题满分12分)如图,在底面是直角梯形的四棱锥P—ABCD中,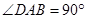 ,
,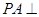 平面ABCD,PA=AB=BC=3,梯形上底AD=1。
平面ABCD,PA=AB=BC=3,梯形上底AD=1。
(1)求证: 平面PAB;
平面PAB;
(2)求面PCD与面PAB所成锐二面角的正切值;
(3)在PC上是否存在一点E,使得DE//平面PAB?若存在,请找出;若不存在,说明理由。

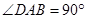 ,
,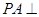 平面ABCD,PA=AB=BC=3,梯形上底AD=1。
平面ABCD,PA=AB=BC=3,梯形上底AD=1。(1)求证:
 平面PAB;
平面PAB;(2)求面PCD与面PAB所成锐二面角的正切值;
(3)在PC上是否存在一点E,使得DE//平面PAB?若存在,请找出;若不存在,说明理由。

(本小题满分12分)
(Ⅰ)证明:由题意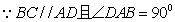
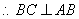
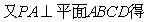


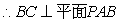 ………………………………… 4分
………………………………… 4分
(Ⅱ)(法一)延长BA、CD交于Q点,过A作AH⊥PQ,垂足为H,连DH
由(Ⅰ)及AD∥BC知:AD⊥平面PAQ
∴ AD⊥PQ且AH⊥PQ
所以PQ⊥平面HAD,即PQ⊥HD.
所以∠AHD是面PCD与面PBA所成的二面角的平面角. …………… 6分
易知 ,所以
,所以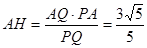
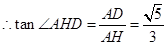
所以面PCD与面PAB所成二面角的正切值为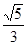 . ………………8分
. ………………8分

(Ⅲ)解:存在. ……………………………………………………9分
在BC上取一点F,使BF=1,则DF∥AB.由条件知,PC=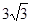 ,在PC上取点E,使PE=
,在PC上取点E,使PE= ,则EF∥PB. ………………10分
,则EF∥PB. ………………10分
所以,平面EFD∥平面PAB
故 DE∥平面PAB …………………………………………………12分
(Ⅰ)证明:由题意
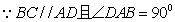
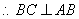
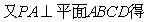


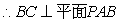 ………………………………… 4分
………………………………… 4分(Ⅱ)(法一)延长BA、CD交于Q点,过A作AH⊥PQ,垂足为H,连DH
由(Ⅰ)及AD∥BC知:AD⊥平面PAQ
∴ AD⊥PQ且AH⊥PQ
所以PQ⊥平面HAD,即PQ⊥HD.
所以∠AHD是面PCD与面PBA所成的二面角的平面角. …………… 6分
易知
 ,所以
,所以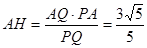
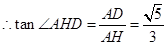
所以面PCD与面PAB所成二面角的正切值为
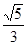 . ………………8分
. ………………8分
(Ⅲ)解:存在. ……………………………………………………9分
在BC上取一点F,使BF=1,则DF∥AB.由条件知,PC=
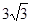 ,在PC上取点E,使PE=
,在PC上取点E,使PE= ,则EF∥PB. ………………10分
,则EF∥PB. ………………10分所以,平面EFD∥平面PAB
故 DE∥平面PAB …………………………………………………12分
略

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
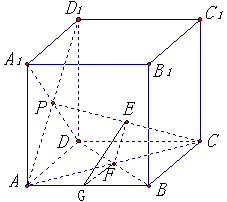
 中,
中, 为侧面
为侧面 的中心,
的中心,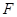 为底面
为底面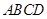 的中心,
的中心,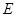 为
为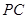 的中点,G为AB的 中点,
的中点,G为AB的 中点,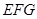 //平面
//平面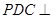 平面
平面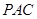 .
.
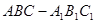 中,
中,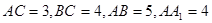 .
.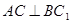 ;(Ⅱ)求二面角
;(Ⅱ)求二面角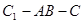 的余弦值大小;
的余弦值大小;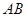 上是否存在点
上是否存在点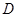 ,使得
,使得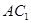 ∥平面
∥平面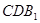 , 若存在,试给出证明;若不存在,请说明理由.
, 若存在,试给出证明;若不存在,请说明理由.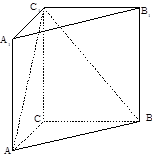
 中,
中,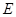 、
、 分别为
分别为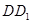 、
、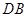 的中点.
的中点.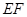 //平面
//平面 ;
;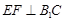 ;
;
 中,
中,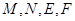 分别是棱
分别是棱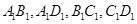 的中点.
的中点. 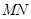 ∥平面
∥平面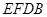 ;
;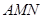 ∥平面
∥平面
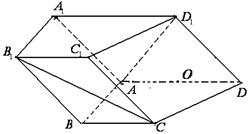
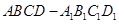 中,侧面
中,侧面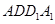 ⊥底面
⊥底面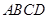 ,
,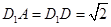 ,底面
,底面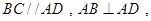
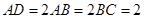 ,O为
,O为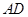 中点。
中点。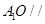 平面
平面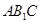 ;
;
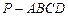 中,四边形
中,四边形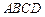 是正方形,
是正方形,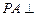 平面
平面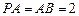 ,且
,且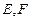 分别是
分别是 的中点.
的中点.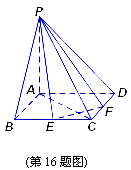
 平面
平面 ;
;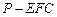 的体积.
的体积.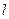 、
、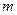 是不同的两条直线,
是不同的两条直线,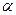 、
、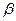 是不重合的两个平面,
是不重合的两个平面,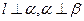 ,则
,则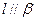
 ,则
,则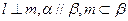 ,则
,则
 ,则
,则