题目内容
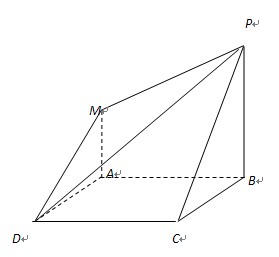
(12分)如图,在底面是直角梯形的四棱锥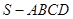 中,
中,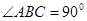 ,
,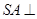 面
面 ,
, ,
,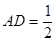 。
。
(1)求证:面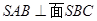 ;
;
(2)求点C到平面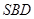 的距离。
的距离。
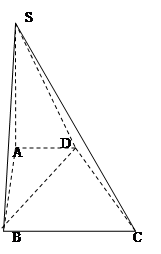
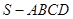 中,
中,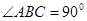 ,
,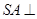 面
面 ,
, ,
,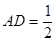 。
。(1)求证:面
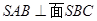 ;
;(2)求点C到平面
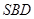 的距离。
的距离。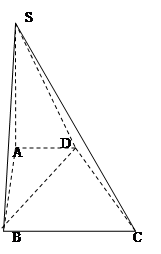
证明:(1)

由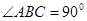 ,
,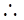
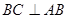 ,而
,而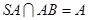
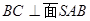 ,而
,而
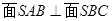
(2)方法不一,答案为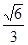 ,设所求距离为
,设所求距离为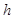 .
.
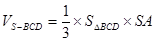 =
=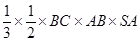 =
=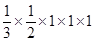 =
=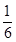
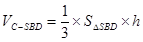
由题易得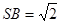 ,
,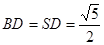 ,于是得
,于是得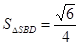
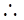
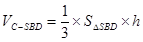 =
=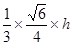
由
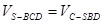 得
得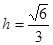
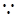
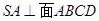
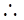

由
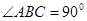 ,
,
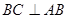 ,而
,而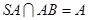
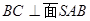 ,而
,而
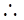
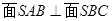
(2)方法不一,答案为
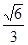 ,设所求距离为
,设所求距离为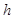 .
.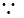
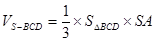 =
=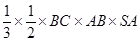 =
=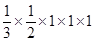 =
=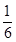
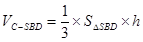
由题易得
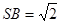 ,
,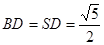 ,于是得
,于是得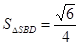
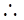
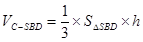 =
=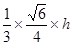
由

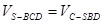 得
得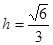
略

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
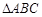 中,D,E,F分别是AB,AC和BC边的中点,
中,D,E,F分别是AB,AC和BC边的中点,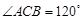 ,现将
,现将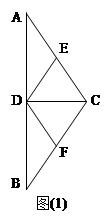
 DE?证明你的结论.
DE?证明你的结论. 是平面,
是平面,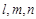 是直线,则下列命题正确的是( )
是直线,则下列命题正确的是( )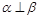 ,
,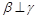 ,则
,则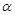 ∥
∥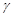
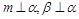 ,则
,则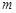 ∥
∥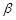
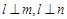 ,则
,则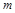 ∥
∥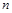
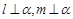 ,则
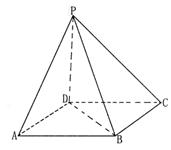
,则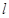 ∥
∥
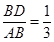
 时,求二面角
时,求二面角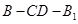 的余弦值.
的余弦值.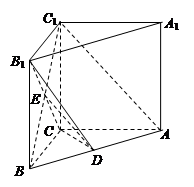
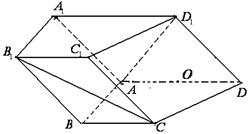
 中,侧面
中,侧面 ⊥底面
⊥底面 ,
,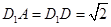 ,底面
,底面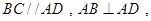
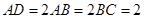 ,O为
,O为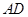 中点。
中点。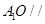 平面
平面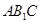 ;
;
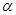 、
、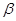 是平面,m、n是直线,则下列命题不正确的是( )
是平面,m、n是直线,则下列命题不正确的是( )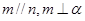 ,则
,则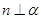
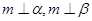 ,则
,则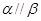
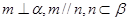 ,则
,则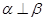
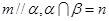 ,则
,则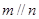
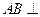 侧面BB1C1C,已知AB=BC=1,BB1=2,
侧面BB1C1C,已知AB=BC=1,BB1=2,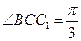 ,E为CC1的中点。
,E为CC1的中点。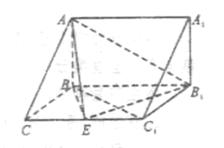
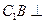 平面ABC;
平面ABC;