题目内容
14．
下列对应关系中是集合A到集合B的函数的个数是（ ）①A=R，B={x|x＞0}，f：x→y=|x|；
②A=Z，B=Z，f：x→y=x2；
③A=Z，B=Z，f：x→y=$\sqrt{x}$；
④A=[-1，1]，B={0}．f：x→y=0；
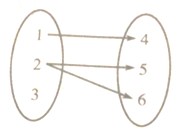
⑤A={1，2，3}，B={4，5，6}，对应关系如图．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据函数的概念和对应关系进行判断即可．
解答 解：①A=R，B={x|x＞0}，f：x→y=|x|不是函数关系，∵当x=0时，|0|=0，|x|＞0不成立，∴不是函数关系；
②A=Z，B=Z，f：x→y=x2是函数关系；
③A=Z，B=Z，f：x→y=$\sqrt{x}$当x＜0时，没有对应关系，故不是函数关系；
④A=[-1，1]，B={0}．f：x→y=0是函数关系；
⑤A={1，2，3}，B={4，5，6}，对应关系如图，3没有元素对应，不是函数关系．
故是函数关系的是②④，共2个，
故选：B．
点评 本题主要考查函数关系的判断，根据函数的定义确定元素之间的对应关系是解决本题的关键．比较基础．
练习册系列答案
相关题目
4．已知复数z=3-2i-$\frac{5i}{2-i}$，则复数z对应复平面上的点Z位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
5．某超市从2014年甲、乙两种酸奶的日销售量（单位：箱）的数据中分別随机抽取100个．整理得到数据分组及频率分布表和频率分布直方图：
（Ⅰ）写出频率分布直方图1中的a的值；并作出甲种酸奶日销售量的频率分布直方图；
（Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为s${\;}_{1}^{2}$，s${\;}_{2}^{2}$，试比较s${\;}_{1}^{2}$与s${\;}_{2}^{2}$的大小；（只需写出结论）
（Ⅲ）假设同一组中的每个数据可用该该组区间的中点值代替，试估计乙种酸奶在未来一个月（按30天计箅）的销售量总量．
| 分组（日销售量） | 频率（甲种酸奶） |
| [0，10] | 0.10 |
| （10，20] | 0.20 |
| （20，30] | 0.30 |
| （30，40] | 0.25 |
| （40，50] | 0.15 |
（Ⅰ）写出频率分布直方图1中的a的值；并作出甲种酸奶日销售量的频率分布直方图；
（Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为s${\;}_{1}^{2}$，s${\;}_{2}^{2}$，试比较s${\;}_{1}^{2}$与s${\;}_{2}^{2}$的大小；（只需写出结论）
（Ⅲ）假设同一组中的每个数据可用该该组区间的中点值代替，试估计乙种酸奶在未来一个月（按30天计箅）的销售量总量．
19．设a、b、c分别是△ABC的三边长，且a=4，b=5，c=7，则△ABC是（ ）
| A． | 直角三角形 | B． | 锐角三角形 | C． | 钝角三角形 | D． | 无法确定 |