题目内容
19.设a、b、c分别是△ABC的三边长,且a=4,b=5,c=7,则△ABC是( )| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 无法确定 |
分析 由题意可得C为最大角,由余弦定理可得cosC的值,可判三角形形状.
解答 解:由三角形大边对大角可得C为最大角,
由余弦定理可得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{{4}^{2}+{5}^{2}-{7}^{2}}{2×4×5}$=-$\frac{1}{5}$<0,
∴C为钝角,△ABC为钝角三角形.
故选:C.
点评 本题考查余弦定理,涉及三角形的三边关系,属基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知双曲线C与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1有相同的焦点F1、F2,点P为双曲线C与椭圆的一个交点,且满足|PF1|=2|PF2|,则双曲线C的渐近线方程是( )
| A. | y=±$\sqrt{3}$x | B. | y=±$\sqrt{2}$x | C. | y=±x | D. | y=±$\frac{\sqrt{3}}{2}$x |
10.如图,有一个几何体的三视图及其尺寸(单位:cm),则该几何体的表面积和体积分别为( )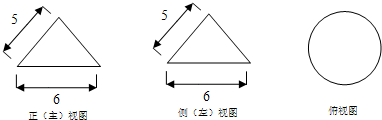

| A. | 24πcm2,12πcm3 | B. | 15πcm2,12πcm3 | C. | 24πcm2,36πcm3 | D. | 15πcm2,36πcm3 |
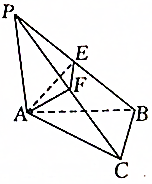 如图所示,已知在△ABC中,∠C=90°,PA⊥平面ABC,AE⊥PB交PB于E,AF⊥PC于F,AP=AB=2,∠AEF=θ,当θ变化时,求三棱锥P-AEF的体积的最大值.
如图所示,已知在△ABC中,∠C=90°,PA⊥平面ABC,AE⊥PB交PB于E,AF⊥PC于F,AP=AB=2,∠AEF=θ,当θ变化时,求三棱锥P-AEF的体积的最大值.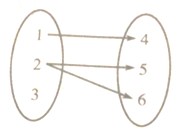 下列对应关系中是集合A到集合B的函数的个数是( )
下列对应关系中是集合A到集合B的函数的个数是( )