题目内容
3.已知抛物线y=x2+2x+b的顶点在椭圆2x2+y2=6上,则b的值是3或-1.分析 求出抛物线的顶点坐标,代入椭圆方程,即可得出结论.
解答 解:抛物线y=x2+2x+b的顶点坐标是(-1,-1+b),
代入椭圆2x2+y2=6可得2+(-1+b)2=6,
所以b=3或-1.
故答案为:3或-1.
点评 本题考查抛物线的性质,考查椭圆方程,考查学生的计算能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.设函数f(x)=2+$\frac{2mx+sinx+mxcosx}{2+cosx}$,若f(x)在[-n,n]上的值域为[a,b],其中a,b,m,n∈R,且n>0,则a+b=( )
| A. | 0 | B. | 2 | C. | 4 | D. | 2m |
12.已知函数f(x)=$\left\{{\begin{array}{l}{{3^{-x}}-1,x≥0}\\{1-{3^x},x<0}\end{array}}$,则该函数是( )
| A. | 偶函数,且单调递增 | B. | 偶函数,且单调递减 | ||
| C. | 奇函数,且单调递增 | D. | 奇函数,且单调递减 |
3.若曲线C在顶点为O的角α的内部,A、B分别是曲线C上相异的任意两点,且α≥∠AOB,我们把满足条件的最小角α叫做曲线C相对点O的“确界角”.已知O为坐标原点,曲线C的方程为y=$\left\{\begin{array}{l}{\sqrt{1+{x}^{2}},x≥0}\\{2-\sqrt{1-{x}^{2}},x<0}\end{array}\right.$,那么它相对点O的“确界角”等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{5π}{12}$ | C. | $\frac{7π}{12}$ | D. | $\frac{2π}{3}$ |
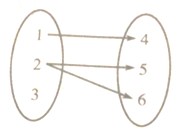 下列对应关系中是集合A到集合B的函数的个数是( )
下列对应关系中是集合A到集合B的函数的个数是( )