题目内容
9.已知向量$\overrightarrow{a}$=(3,0),向量$\overrightarrow{b}$=(k,5)且向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是135°,求k的值.分析 由题意可得cos135°=-$\frac{\sqrt{2}}{2}$=$\frac{3k+0}{3\sqrt{{k}^{2}+25}}$,由此求得k的值.
解答 解:由题意可得cos135°=-cos45°=-$\frac{\sqrt{2}}{2}$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{3k+0}{3\sqrt{{k}^{2}+25}}$,
求得k=-5.
点评 本题主要考查用两个向量的数量积表示两个向量的夹角,两个向量的数量积的定义,属于基础题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
17.若实数a,b满足a2+b2≤1,则关于x的方程x2-ax+$\frac{3}{4}$b2=0有实数根的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | 1 |
4.已知函数f(x)满足f(x+4)=f(x),且当-1<x≤3时,f(x)=$\left\{\begin{array}{l}{m\sqrt{1-{x}^{2}},x∈(-1,1]}\\{1-|x-2|,x∈(1,3]}\end{array}\right.$.其中m>0,若方程3f(x)-x=0恰好有5个根,则实数m的取值范围是( )
| A. | ($\frac{\sqrt{15}}{3}$,$\sqrt{7}$) | B. | ($\frac{\sqrt{15}}{3}$,$\frac{8}{3}$) | C. | ($\frac{4}{3}$,$\sqrt{7}$) | D. | ( $\frac{4}{3}$,$\frac{8}{3}$) |
1.设复数z1=-1+i,z2=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i,则$\frac{{z}_{1}}{{z}_{2}}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
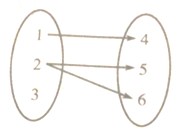 下列对应关系中是集合A到集合B的函数的个数是( )
下列对应关系中是集合A到集合B的函数的个数是( )