题目内容
2.函数y=$\frac{1}{3}$x3-3x的图象上,其任意点处的切线倾斜角小于$\frac{π}{4}$的点中,坐标为整数的点的个数是0.分析 根据倾斜角求出斜率的范围,设出切点坐标,利用导数的函数值就是该点的斜率,求出切点横坐标的范围,即可推出坐标为整数的点的个数.
解答 解:∵切线倾斜角小于$\frac{π}{4}$,
∴斜率0≤k<1.
设切点为(x0,$\frac{1}{3}$x03-3x0),则k=y′|x=x0=x02-3,
∴0≤x02-3<1,3≤x02<4.
又∵x0∈Z,∴x0不存在.
故答案为:0.
点评 本题考查直线的斜率、导数的运算,考查计算能力,逻辑思维能力,是基础题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
12.把函数y=sin(2x+$\frac{π}{6}$)的图象向右平移$\frac{π}{6}$个单位得到函数f(x)的图象,则下列说法正确的是( )
| A. | f(x)的图象关于y轴对称 | B. | f(x)的图象关于原点对称 | ||
| C. | f(x)的图象关于直线x=$\frac{π}{3}$对称 | D. | f(x)的图象关于点($\frac{π}{3}$,0)对称 |
10.如图,有一个几何体的三视图及其尺寸(单位:cm),则该几何体的表面积和体积分别为( )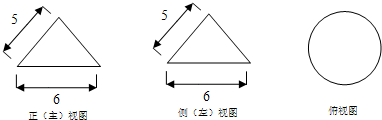

| A. | 24πcm2,12πcm3 | B. | 15πcm2,12πcm3 | C. | 24πcm2,36πcm3 | D. | 15πcm2,36πcm3 |
17.若实数a,b满足a2+b2≤1,则关于x的方程x2-ax+$\frac{3}{4}$b2=0有实数根的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | 1 |
11.设函数f(x)=2+$\frac{2mx+sinx+mxcosx}{2+cosx}$,若f(x)在[-n,n]上的值域为[a,b],其中a,b,m,n∈R,且n>0,则a+b=( )
| A. | 0 | B. | 2 | C. | 4 | D. | 2m |
12.已知函数f(x)=$\left\{{\begin{array}{l}{{3^{-x}}-1,x≥0}\\{1-{3^x},x<0}\end{array}}$,则该函数是( )
| A. | 偶函数,且单调递增 | B. | 偶函数,且单调递减 | ||
| C. | 奇函数,且单调递增 | D. | 奇函数,且单调递减 |
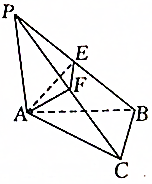 如图所示,已知在△ABC中,∠C=90°,PA⊥平面ABC,AE⊥PB交PB于E,AF⊥PC于F,AP=AB=2,∠AEF=θ,当θ变化时,求三棱锥P-AEF的体积的最大值.
如图所示,已知在△ABC中,∠C=90°,PA⊥平面ABC,AE⊥PB交PB于E,AF⊥PC于F,AP=AB=2,∠AEF=θ,当θ变化时,求三棱锥P-AEF的体积的最大值.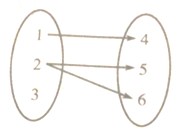 下列对应关系中是集合A到集合B的函数的个数是( )
下列对应关系中是集合A到集合B的函数的个数是( )