题目内容

4．已知复数z=3-2i-$\frac{5i}{2-i}$，则复数z对应复平面上的点Z位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 利用复数代数形式的乘除运算化简，求出z的坐标得答案．

解答 解：∵z=3-2i-$\frac{5i}{2-i}$=$3-2i-\frac{5i（2+i）}{（2-i）（2+i）}=3-2i-\frac{-5+10i}{5}$=3-2i+1-2i=4-4i，
∴复数z对应复平面上的点Z的坐标为（4，-4），位于第四象限．
故选：D．

点评 本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．

练习册系列答案
相关题目
14．已知函数f（x）=$\left\{\begin{array}{l}a•{2^x}（x≤0）\\{log_2}x（x＞0）\end{array}$，若关于x的方程f[f（x）]=0有且只有一个实数根，则实数a的取值范围是（　　）
A．（-∞，0）B．（-∞，0）∪（0，1）C．（0，1）D．（0，1）∪（1，+∞）
15．设某几何体的三视图如图，则该几何体的体积为4
12．把函数y=sin（2x+$\frac{π}{6}$）的图象向右平移$\frac{π}{6}$个单位得到函数f（x）的图象，则下列说法正确的是（　　）
A．f（x）的图象关于y轴对称B．f（x）的图象关于原点对称
C．f（x）的图象关于直线x=$\frac{π}{3}$对称D．f（x）的图象关于点（$\frac{π}{3}$，0）对称
19．已知$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$是同一平面内的三个向量，其中$\overrightarrow{a}$=（2，1）．
（1）若|$\overrightarrow{c}$|=3$\sqrt{5}$，且$\overrightarrow{c}$∥$\overrightarrow{a}$，求$\overrightarrow{c}$的坐标；
（2）若|$\overrightarrow{b}$|=$\frac{\sqrt{5}}{2}$，且$\overrightarrow{a}$+2$\overrightarrow{b}$与2$\overrightarrow{a}$-$\overrightarrow{b}$垂直，求$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ．
9．已知双曲线C与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1有相同的焦点F1、F2，点P为双曲线C与椭圆的一个交点，且满足|PF1|=2|PF2|，则双曲线C的渐近线方程是（　　）
A．y=±$\sqrt{3}$xB．y=±$\sqrt{2}$xC．y=±xD．y=±$\frac{\sqrt{3}}{2}$x
16．已知函数f（x）=lnx+$\frac{ax}{x+1}$，其中a为实常数．
（Ⅰ）当a=1时，计算由曲线y=f（x）-lnx和直线x=0，x=2以及x轴所围图形的面积S；
（Ⅱ）若f（x）在（0，+∞）上是增函数，求a的取范围；
（Ⅲ）若f（x）有两个不同的极值点x1，x2，当x＞0时，比较$\frac{f（{x}_{1}）+f（{x}_{2}）}{x+1}$与$\frac{f（x）-x+1}{x}$的大小．
13．圆C：x2+y2=4关于直线x+2y-5=0对称的圆的方程为（x-2）2+（y-4）2=4．
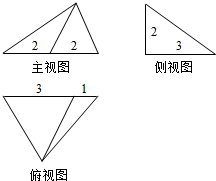
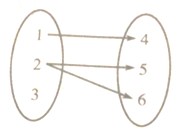14．下列对应关系中是集合A到集合B的函数的个数是（　　）
①A=R，B={x|x＞0}，f：x→y=|x|；
②A=Z，B=Z，f：x→y=x2；
③A=Z，B=Z，f：x→y=$\sqrt{x}$；
④A=[-1，1]，B={0}．f：x→y=0；
⑤A={1，2，3}，B={4，5，6}，对应关系如图．
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网