题目内容
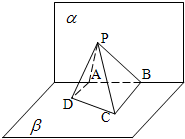
在三棱锥A-BCD中,AB,AC,AD两两互相垂直,AB=AC=AD=4.点P,Q分别在侧面ABC,棱AD上运动.PQ=2,M为线段PQ的中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成两部分的体积之比等于( )
| A.1:63 | B.1:(16
| C.π:(64-π) | D.π:(14-π) |
∵AD⊥AB,AD⊥AC,AB∩AC=A,∴AD⊥平面ABC,AP?平面ABC,
∴△PAQ为直角三角形,M为斜边PQ的中点,∴AM=
PQ=1,
∴M的轨迹是以A为球心,1为半径的八分之一球面,
V1=
×
π×13=
,V2=
×
×4×4×4-
=
,
∴
=
.
故选C.
∴△PAQ为直角三角形,M为斜边PQ的中点,∴AM=
| 1 |
| 2 |
∴M的轨迹是以A为球心,1为半径的八分之一球面,
V1=
| 1 |
| 8 |
| 4 |
| 3 |
| π |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| 64-π |
| 6 |
∴
| V1 |
| V2 |
| π |
| 64-π |
故选C.

练习册系列答案
相关题目