题目内容
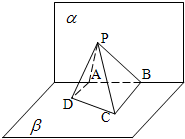
如图,已知平面α∩β=l,A、B是l上的两个点,C、D在平面β内,且DA⊥α,CB⊥α,AD=4,AB=6,BC=8,在平面α上有一个动点P,使得∠APD=∠BPC,则P-ABCD体积的最大值是( )
A.24
| B.16 | C.48 | D.144 |

由题意平面α⊥平面β,A、B是平面α与平面β的交线上的两个定点,DA?β,CB?β,且DA⊥α,CB⊥α,
∴△PAD与△PBC是直角三角形,又∠APD=∠BPC,∴△PAD∽△PBC,又AD=4,BC=8,∴PB=2PA.
作PM⊥AB,垂足为M,则PM⊥β,令AM=t∈R,在两个Rt△PAM与Rt△PBM中,PM是公共边及PB=2PA,∴PA2-t2=4PA2-(6-t)2 ,解得PA2=12-4t.
∴PM=
,即四棱锥的高为
,底面为直角梯形,S=
×(4+8)×6=36
∴四棱锥P-ABCD的体积V=
×36×
=12
≤12×
=48,
即四棱锥P-ABCD体积的最大值为48,
故选C.
∴△PAD与△PBC是直角三角形,又∠APD=∠BPC,∴△PAD∽△PBC,又AD=4,BC=8,∴PB=2PA.
作PM⊥AB,垂足为M,则PM⊥β,令AM=t∈R,在两个Rt△PAM与Rt△PBM中,PM是公共边及PB=2PA,∴PA2-t2=4PA2-(6-t)2 ,解得PA2=12-4t.
∴PM=
| 12-4t-t2 |
| 12-4t-t2 |
| 1 |
| 2 |
∴四棱锥P-ABCD的体积V=
| 1 |
| 3 |
| 12-4t-t2 |
| 16-(t+2)2 |
| 16 |
即四棱锥P-ABCD体积的最大值为48,
故选C.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目