题目内容
【题目】已知三点A(1,﹣1),B(3,0),C(2,1),P为平面ABC上的一点, ![]() =λ
=λ ![]() +μ
+μ ![]() ,且
,且 ![]()
![]() =0,
=0, ![]()
![]() =3.
=3.
(1)求 ![]()
![]() ;
;
(2)求λ+μ 的值.
【答案】
(1)解: ![]() =(2,1),
=(2,1), ![]() =(1,2),
=(1,2),
∴ ![]() =2×1+1×2=4
=2×1+1×2=4
(2)解: ![]() =λ
=λ ![]() +μ
+μ ![]() =(2λ+μ,λ+2μ),
=(2λ+μ,λ+2μ),
∵ 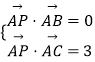 ,∴
,∴ ![]() ,即
,即 ![]() ,
,
两式相加得:9λ+9μ=3,
∴λ+μ= ![]()
【解析】(1)求出 ![]() 的坐标,代入向量的坐标运算公式计算数量积;(2)用λ,μ表示出
的坐标,代入向量的坐标运算公式计算数量积;(2)用λ,μ表示出 ![]() 的坐标,根据向量的数量积公式列方程组求出λ+μ.
的坐标,根据向量的数量积公式列方程组求出λ+μ.
【考点精析】根据题目的已知条件,利用平面向量的基本定理及其意义的相关知识可以得到问题的答案,需要掌握如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() .
.

 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】已知球O是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A﹣BCD的外接球,BC=3,AB=2 ![]() ,点E在线段BD上,且BD=3BE,过点E作球O的截面,则所得截面圆面积的取值范围是 .
,点E在线段BD上,且BD=3BE,过点E作球O的截面,则所得截面圆面积的取值范围是 .
【题目】某校期中考试后,按照学生的数学考试成绩优秀和不优秀进行统计,得到如下列联表:
优秀 | 不优秀 | 总计 | |
文科 | 60 | 140 | 200 |
理科 | 265 | 335 | 600 |
总计 | 325 | 475 | 800 |
(1)画出列联表的等高条形图,并通过图形判断数学成绩与文理分科是否有关;
(2)利用独立性检验,分析文理分科对学生的数学成绩是否有影响.
【题目】2016年备受瞩目的二十国集团领导人第十一次峰会于9月4~5日在杭州举办,杭州G20筹委会已经招募培训翻译联络员1000人、驾驶员2000人,为测试培训效果,采取分层抽样的方法从翻译联络员、驾驶员中共随机抽取60人,对其做G20峰会主题及相关服务职责进行测试,将其所得分数(分数都在60~100之间)制成频率分布直方图如下图所示,若得分在90分及其以上(含90分)者,则称其为“G20通”. 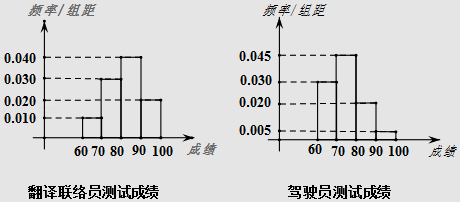
(Ⅰ)能否有90%的把握认为“G20通”与所从事工作(翻译联络员或驾驶员)有关?
(Ⅱ)从参加测试的成绩在80分以上(含80分)的驾驶员中随机抽取4人,4人中“G20通”的人数为随机变量X,求X的分布列与数学期望.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
附参考公式与数据: ![]() .
.
【题目】在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下:
成绩/m | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 | 1.85 | 1.90 |
人数 | 2 | 3 | 2 | 3 | 4 | 1 | 1 | 1 |
分别求这些运动员的成绩的众数、中位数、平均数(保留到小数点后两位),并分析这些数据的含义.

