Question

【题目】已知函数f（x）=1﹣ ﹣lnx（a∈R）．
（1）当a=1时，求函数f（x）的图象在点（ ，f（ ））处的切线方程；
（2）当a≥0时，记函数Γ（x）= ax2+（1﹣2a）x+ ﹣1+f（x），试求Γ（x）的单调递减区间；
（3）设函数h（a）=3λa﹣2a2（其中λ为常数），若函数f（x）在区间（0，2）上不存在极值，求h（a）的最大值．

Answer 1

【答案】
（1）解：当a=1时， ， ，

则 ， ∴函数f（x）的图象在点 的切线方程为： ，

即2x﹣y+ln2﹣2=0．

（2）解：∵ ，∴ （x＞0）， ，

①当a=0时， ，

由 及x＞0可得：0＜x≤1，∴Γ（x）的单调递减区间为（0，1]

②当a＞0时， ，

由ax2﹣（2a﹣1）x﹣1=0可得：△=（2a﹣1）2+4a=4a2+1＞0，

设其两根为x1，x2，因为 ，所以x1，x2一正一负，

设其正根为x2，则 ，

由 及x＞0可得： ，∴Γ（x）的单调递减区间为 ．

（3）解： ，由f'（x）=0x=a，

由于函数f（x）在区间（0，2）上不存在极值，所以a≤0或a≥2…（10分）对于h（a）=3λa﹣2a2，对称轴 ，

当 或 ，即λ≤0或 时， ；

当 ，即 时，h（a）max=h（0）=0；

当 ，即 时，h（a）max=h（2）=6λ﹣8；

综上可知：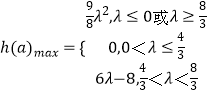

【解析】（1）当a=1时，化简函数的解析式求出函数的导数，求出斜率以及切点坐标，求解切线方程．（2）化简函数Γ（x）= ﹣1+f（x）的解析式，求出函数的导数，通过①当a=0时，②当a＞0时，分别通过函数的极值点，判断函数的单调性．求出单调区间．（3）通过函数的导数为0，求出极值点，利用题意转化为函数f（x）在区间（0，2）上不存在极值，求出a的范围然后求解h（a）max值即可．
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本，需要知道一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．