题目内容
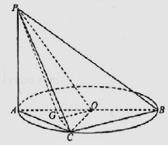
【题目】已知球O是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A﹣BCD的外接球,BC=3,AB=2 ![]() ,点E在线段BD上,且BD=3BE,过点E作球O的截面,则所得截面圆面积的取值范围是 .
,点E在线段BD上,且BD=3BE,过点E作球O的截面,则所得截面圆面积的取值范围是 .
【答案】[2π,4π]
【解析】解:如图,设△BDC的中心为O1 , 球O的半径为R, 连接oO1D,OD,O1E,OE,
则 ![]() ,AO1=
,AO1= ![]() ,
,
在Rt△OO1D中,R2=3+(3﹣R)2 , 解得R=2,
∵BD=3BE,∴DE=2
在△DEO1中,O1E= ![]()
∴ ![]()
过点E作圆O的截面,当截面与OE垂直时,截面的面积最小,
此时截面圆的半径为 ![]() ,最小面积为2π.
,最小面积为2π.
当截面过球心时,截面面积最大,最大面积为4π.
所以答案是[2π,4π]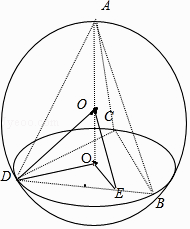
【考点精析】本题主要考查了球内接多面体的相关知识点,需要掌握球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长才能正确解答此题.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案【题目】有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 105 |
已知在全部105人中随机抽取一人为优秀的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,若按97.5%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到10或11号的概率.
参考公式和数据: ![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
【题目】某单位员工![]() 人参加“学雷锋”志愿活动,按年龄分组:第
人参加“学雷锋”志愿活动,按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)下表是年龄的频率分布表,求正整数![]() 的值;
的值;
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
(2)现在要从年龄较小的第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,年龄在第
人,年龄在第![]() 组抽取的员工的人数分别是多少?
组抽取的员工的人数分别是多少?
(3)在(2)的前提下,从这![]() 人中随机抽取
人中随机抽取![]() 人参加社区宣传交流活动,求至少有
人参加社区宣传交流活动,求至少有![]() 人年龄在第
人年龄在第![]() 组的概率.
组的概率.